Problem statement
Given the coordinates of two rectilinear rectangles in a 2D plane, return the total area covered by the two rectangles.
The first rectangle is defined by its bottom-left corner (ax1, ay1) and its top-right corner (ax2, ay2).
The second rectangle is defined by its bottom-left corner (bx1, by1) and its top-right corner (bx2, by2).
Problem statement taken from: https://leetcode.com/problems/rectangle-area
Example 1:
Input: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
Output: 45
Example 2:
Input: ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
Output: 16
Constraints:
- -10^4 <= ax1 <= ax2 <= 10^4
- -10^4 <= ay1 <= ay2 <= 10^4
- -10^4 <= bx1 <= bx2 <= 10^4
- -10^4 <= by1 <= by2 <= 10^4
Explanation
The solution to this problem is straightforward. We need to use the school mathematical concept to get the area of two rectangles.
area = Area of rectangle 1 + Area of rectangle 2 - Area of intersecting portion
To calculate the area of intersecting part, we need to compute below four coordinates:
maxCommonX = max(ax1, bx1)
maxCommonY = max(ay1, by1)
minCommonX = min(ax2, bx2)
minCommonY = min(ay2, by2)
commonArea = (minCommonX - maxCommonX) * (minCommonY - maxCommonY)
Let's check the algorithm.
// compute the area of rectangles using L * H
- set area1 = (ax2 - ax1) * (ay2 - ay1)
set area2 = (bx2 - by1) * (by2 - by1)
// if the rectangles do not intersect, return area1 + area2
- if bx1 >= ax2 || bx2 <= ax1 || by1 >= ay2 || by2 <= ay1
- return area1 + area2
- set maxCommonX = max(ax1, bx1)
set maxCommonY = max(ay1, by1)
- set minCommonX = min(ax2, bx2)
set minCommonY = min(ay2, by2)
- return area1 + area2 - (minCommonX - maxCommonX) * (minCommonY - maxCommonY);
Let's check our algorithm in C++, Golang, and Javascript.
C++ solution
class Solution {
public:
int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
int area1 = (ax2 - ax1) * (ay2 - ay1);
int area2 = (bx2 - bx1) * (by2 - by1);
if(bx1 >= ax2 || bx2 <= ax1 || by1 >= ay2 || by2 <= ay1) {
return area1 + area2;
}
int maxCommonX = max(ax1, bx1);
int maxCommonY = max(ay1, by1);
int minCommonX = min(ax2, bx2);
int minCommonY = min(ay2, by2);
return area1 + area2 - (minCommonX - maxCommonX) * (minCommonY - maxCommonY);
}
};
Golang solution
func computeArea(ax1 int, ay1 int, ax2 int, ay2 int, bx1 int, by1 int, bx2 int, by2 int) int {
area1 := (ax2 - ax1) * (ay2 - ay1)
area2 := (bx2 - bx1) * (by2 - by1)
if bx1 >= ax2 || bx2 <= ax1 || by1 >= ay2 || by2 <= ay1 {
return area1 + area2;
}
maxCommonX := max(ax1, bx1)
maxCommonY := max(ay1, by1)
minCommonX := min(ax2, bx2)
minCommonY := min(ay2, by2)
return area1 + area2 - (minCommonX - maxCommonX) * (minCommonY - maxCommonY)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
Javascript solution
var computeArea = function(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2) {
let area1 = (ax2 - ax1) * (ay2 - ay1);
let area2 = (bx2 - bx1) * (by2 - by1);
if(bx1 >= ax2 || bx2 <= ax1 || by1 >= ay2 || by2 <= ay1) {
return area1 + area2;
}
let maxCommonX = Math.max(ax1, bx1);
let maxCommonY = Math.max(ay1, by1);
let minCommonX = Math.min(ax2, bx2);
let minCommonY = Math.min(ay2, by2);
return area1 + area2 - (minCommonX - maxCommonX) * (minCommonY - maxCommonY) ;
};
Let's dry-run our algorithm for Example 1.
Input: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
Step 1: area1 = (ax2 - ax1) * (ay2 - ay1)
= (3 - -3) * (4 - 0)
= 6 * 4
= 24
area2 = (bx2 - bx1) * (by2 - by1)
= (9 - 0) * (2 - -1)
= 9 * 3
= 27
Step 2: if bx1 >= ax2 || bx2 <= ax1 || by1 >= ay2 || by2 <= ay1
0 >= 3 || 9 <= -3 || -1 >= 4 || 2 <= 0
false
Step 3: maxCommonX = max(ax1, bx1)
= max(-3, 0)
= 0
maxCommonY = max(ay1, by1)
= max(0, -1)
= 0
Step 4: minCommonX = min(ax2, bx2)
= min(3, 9)
= 3
minCommonY = min(ay2, by2)
= min(4, 2)
= 2
Step 5: return area1 + area2 - (minCommonX - maxCommonX) * (minCommonY - maxCommonY)
24 + 27 - (3 - 0) * (2 - 0)
51 - 3*2
51 - 6
45
We return the answer as 45.

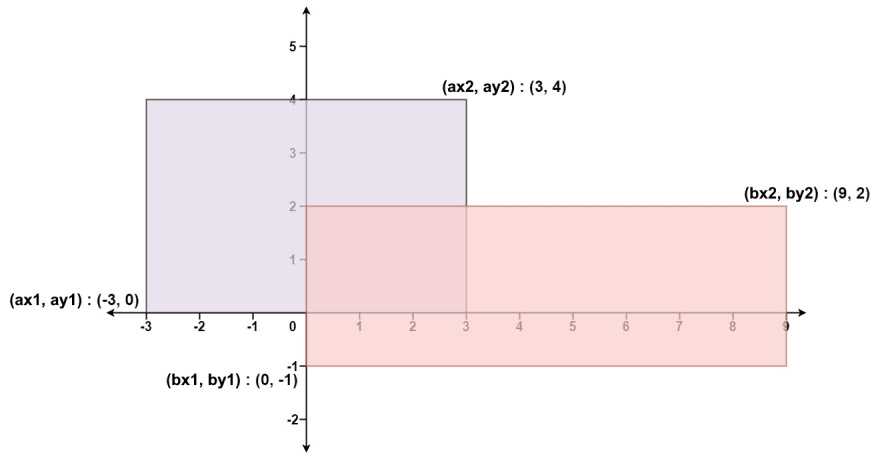





Top comments (0)