¿Deberíamos reimplementar nuestra aplicación, o parte de ella, en un lenguaje más rápido? ¿Tendríamos que dar más recursos a nuestras máquinas? ¿Habría, incluso, que plantear un cambio de arquitectura y optar por una que facilite el paralelismo? Todas ellas son preguntas que nos hemos planteado alguna vez, especialmente cuando nuestra aplicación incrementa el uso de recursos y el rendimiento del sistema se degrada. En este tipo de situaciones, antes de inclinarse por una opción u otra, conviene averiguar cuál es la raíz del problema proponer una solución que actúe sobre dicha raíz.
En este post se explora una de las causas que ralentizan nuestras aplicaciones: la complejidad algorítmica. ¿Cómo varía el tiempo de ejecución al variar el número de datos a procesar? ¿Y los recursos del sistema, como la RAM o CPU? Veremos que, en función de cómo aumente el tiempo de ejecución al incrementar el tamaño de los datos de entrada, tendremos que nuestro algoritmo se comporta de manera:
- Constante: los recursos que emplea el algoritmo no dependen del tamaño de los datos
- Lineal: los recursos necesarios aumentan de manera lineal al tamaño de los datos (ej.: el doble de datos, el doble de tiempo)
- Logarítmico: el incremento de tiempo sigue una respuesta logarítmica
- Cuadrático: los recursos incrementan de manera cuadrática con el número de elementos en el conjunto de datos de la entrada
Sin pérdida de generalidad veamos un ejemplo concreto: dado un array de números, se pide obtener los índices de par de números que suman un determinado valor. Si bien se trata de un ejemplo ilustrativo, es trasladable a una aplicación real. Los casos donde tenemos que recorrer un array y relacionarlo con alguno o algunos de los demás elementos son muy comunes, por ejemplo, en procesado de imágenes, procesado de datos de información geográfica, algoritmos de compresión, etc.
Partamos del siguiente array:
[1, 2, 3, 5]
si el valor buscado es el 7 la solución será (1, 3), ya que el 2 y el 5 son los únicos elementos que suman 7. ¿Cuál sería la lógica del algoritmo para resolver este problema? Veamos varias alternativas y analicemos cuál es su rendimiento.
A menudo la primera opción que se nos ocurre para este tipo de problemas es la llamada comúnmemente fuerza bruta y consiste en analizar todas las combinaciones posibles. Para cada elemento del array, que llamaremos elemento de referencia, buscaremos si hay algún número que sume 7 con el número de referencia. Para el caso que nos ocupa:
- empezamos con el
1como referencia y recorremos el resto de elementos buscando un6, esto es, el complementario para que la suma de ambos sea7 -
en la segunda iteración la referencia es
2, por lo que buscamos un5, que encontraremos en la última posición del array.function searchPairSimple(data, target) { for (i = 0; i < data.length; i++) { for (j = 0; j < data.length; j++) { if (i == j) continue; if (data[i] + data[j] === target) { return [i, j]; } } } }
Los tiempos de ejecución para esta solución en función del número de elementos del array son:
| Tamaño | Algoritmo básico |
|---|---|
| 250 | 0.64 |
| 500 | 0.75 |
| 1000 | 2.98 |
| 2000 | 12.03 |
| 4000 | 47.7 |
¿Cómo podemos mejorar el rendimiento de esta solución? Fijémonos en el segundo bucle. Empieza en el cero, lo que significa que se van a probar combinaciones que ya se habían probado. Por ejemplo, cuando la i valía 0 y la j 1, los valores que teníamos eran el 1 y 2, que suman 3, y por tanto no cumplen la condición buscada. Ahora bien, cuando la i vale 1 y la j vale 0, los valores vuelven a ser el 1 y el 2. Volver a probar pares que ya habían sido descartados es una pérdida de tiempo y recursos, ¿es posible evitarlo? Basta inicializar la j del segundo bucle al valor siguiente de la i. De esta manera las iteracciones se reducen a la mitad.
function searchPairSimpleOptimized(data, target) {
for (i = 0; i < data.length - 1; i++) {
for (j = i+1; j < data.length; j++) {
if (data[i] + data[j] === target) {
return [i, j];
}
}
}
}
| Tamaño | Algoritmo básico |
Algoritmo microoptimizado |
|---|---|---|
| 250 | 0.64 | 0.48 |
| 500 | 0.75 | 0.38 |
| 1000 | 2.98 | 1.47 |
| 2000 | 12.03 | 5.83 |
| 4000 | 47.7 | 23.27 |
¿Es posible mejorarlo aún más? Fijémonos en el último valor del array, el 5. Se ha leído tantas veces como longitud tiene el array, es decir, en cada pasada por el array lo estamos leyendo otra vez. Con el resto de número pasa algo similar: cuanto más a la derecha se encuentren, más veces se habrán leído. ¿Habría forma de leerlos una sola vez? Es decir, cuando estemos en cualquier posición del array, ¿podríamos saber si existe el número complementario sin necesidad de volver a recorrerlo? Dicho de otra forma, ¿podríamos memorizar el contenido del array para no tener que recorrerlo más? La respuesta es sí. Veamos el siguiente código:
function searchPairDictionary(data, target) {
let dict = {}
for (let i = 0; i < data.length; i++) {
dict[data[i]] = i;
if (dict[ target - data[i] ] !== undefined &&
dict[ target - data[i] ] !== i) {
return [i, dict[ target - data[i]]];
}
}
}
La idea es la siguiente: al mismo tiempo que recorremos el array vamos almacenando los valores leídos en un diccionario, cuya clave es el valor que hay en la posición actual del array, y el valor es el índice en el que se encuentra. ¿Por qué esta estructura? La clave es lo que usamos para buscar, mientras que el valor es lo que buscamos: la posición del elemento en el array. Así, cuando hayamos leído el valor 1 del array podremos 'preguntarle' al diccionario si tiene un 6. De esta forma ahorramos volver a iterar sobre todo el array.
| Tamaño | Algoritmo básico |
Algoritmo microoptimizado |
Diccionario |
|---|---|---|---|
| 250 | 0.64 | 0.48 | 0.1 |
| 500 | 0.75 | 0.38 | 0.1 |
| 1000 | 2.98 | 1.47 | 0.23 |
| 2000 | 12.03 | 5.83 | 0.54 |
| 4000 | 47.7 | 23.27 | 0.59 |
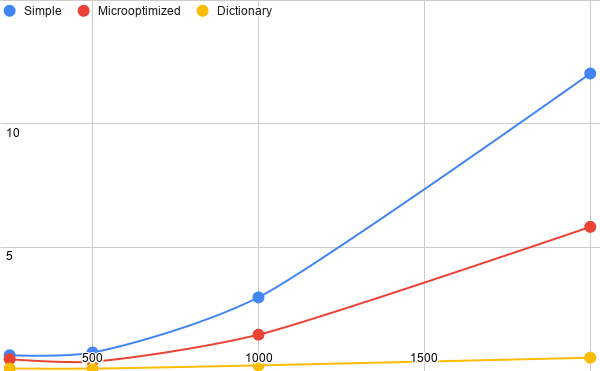
El tiempo de ejecución ha mejorado, especialmente cuando el tamaño del array crece. Además, comparándolo con los tiempos de las dos versiones anteriores del algoritmo la mejora es todavía mayor. Se trata pues, de un buen ejemplo, de cómo cambiando la lógica de nuestra aplicación es posible mejorar mucho el rendimiento sin necesidad de ampliar los recursos disponibles o de emplear arquitecturas software complejas. Si bien, esta mejora no ha sido a coste cero ya que, a diferencia de las otras soluciones, estamos empleando más memoria, la necesaria para el diccionario.
La siguiente imagen representa gráficamente la evolución de los tiempos:
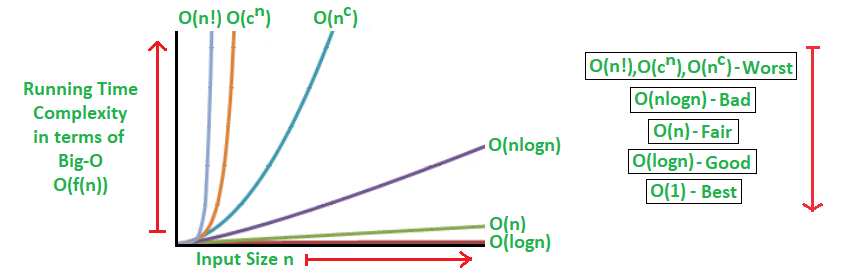
Es buena práctica tener siempre en mente cuál es la complejidad algorítmica de nuestro código. La notación big O, que indica cuál es el orden de mágnitud máximo de nuestro algoritmo, es una de las más extendidas. Así, un algoritmo O(n^2) tardará, como mucho, el cuadrado del tiempo de ejecución de un elemento, pero podría ser menos. La siguiente gráfica muestra cómo evolucionan los tiempos de varios
(https://www.geeksforgeeks.org/analysis-algorithms-big-o-analysis/)






Top comments (0)