Grafos são estruturas de dados que consistem em vértices (ou nós) conectados por arestas (ou arcos). Eles são amplamente utilizados em várias áreas, como ciência da computação, matemática, física, biologia, entre outras.
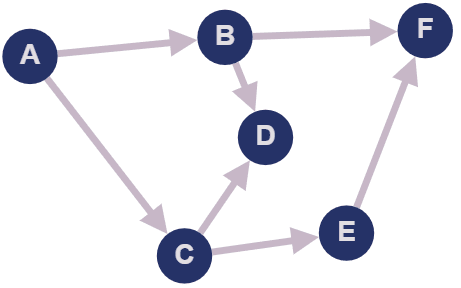
Na ciência da computação, por exemplo, os grafos são usados para representar relações entre objetos, como usuários em uma rede social, ou para modelar rotas e caminhos em mapas, como as ruas no Google Maps. Eles permitem a análise de dados complexos, possibilitando a descoberta de padrões e informações úteis. Vejamos o seguinte grafo:
Para responder perguntas como "existe um caminho do vértice A ao vértice B?" ou "qual é o caminho mínimo do vértice A ao vértice B?", uma das soluções é utilizar o algoritmo de pesquisa em largura (BFS - breadth-first search). Ele começa no vértice A e expande sua pesquisa para os vértices conectados a ele, que são B e C. Em seguida, avança para os vértices conectados a B e C, e assim por diante, buscando em largura.
Vamos criar um exemplo de algoritmo de pesquisa em largura usando JavaScript, para responder a seguinte questão: Qual o caminho mais curto do vértice A ao vértice F?
Primeiro vamos definir as vértices e suas conexões como um objeto:
const connections = {
A: [ 'B', 'C' ],
B: [ 'A', 'D', 'F' ],
C: [ 'A', 'D', 'E' ],
D: [ 'B', 'C' ],
F: [ 'B', 'E' ],
E: [ 'C', 'F' ]
}
Estamos dizendo que A se conecta com B e C, que B se conecta com A, D e F e assim sucessivamente.
Agora vamos começar a criar nosso algoritmo. Primeiro precisamos que ele faça um loop por todos os vértices do grafo e identifique quais já foram visitados.
function findShortestPath(graph, startNode, endNode) {
// fila dos vertices que serão visitados
const queue = [startNode];
// objeto contendo os vértices que já foram visitados
const visited = { [startNode]: true };
// objeto que vai identificar quais os vértices anteriores a um determinado vértice pra montarmos o caminho
const predecessor = {};
// Loop enquanto houverem vértices para ser visitados
while (queue.length) {
// Obtém e remove o primeiro vértice da lista
const currNode = queue.shift();
// RESTO DO NOSSO ALGORITMO
}
return null;
}
Agora precisamos fazer com que, a cada novo vértice buscado, a função obtenha o vértice anterior que se ligue a ele e adicione o caminho no nosso objeto predecessor.
function findShortestPath(graph, startNode, endNode) {
const queue = [startNode];
const visited = { [startNode]: true };
const predecessor = {};
while (queue.length) {
const currNode = queue.shift();
// Obtém os vértices que estão conectados ao vértice atual
// aqui são chamados de vizinhos
const neighbors = graph[currNode];
// Itera sobre cada vértice vizinho
for (const neighbor of neighbors) {
// Apenas continua a busca se ele ainda não tiver sido visitado
if (!visited[neighbor]) {
visited[neighbor] = true;
// Adiciona no objeto predecessor o vértice que está ligado a ele
predecessor[neighbor] = currNode;
// Adiciona ele mesmo na fila de vértices para serem pesquisados
queue.push(neighbor);
// RESTO DO NOSSO ALGORITMO
}
}
}
Agora que o algoritmo já busca todos os vértices do nosso grafo, precisamos fazer com que ele obtenha o vértice de destino e, a partir do objeto predecessor, construa o caminho de volta ao ponto inicial.
function findShortestPath(graph, startNode, endNode) {
const queue = [startNode];
const visited = { [startNode]: true };
const predecessor = {};
while (queue.length) {
const currNode = queue.shift();
const neighbors = graph[currNode];
for (const neighbor of neighbors) {
if (!visited[neighbor]) {
visited[neighbor] = true;
predecessor[neighbor] = currNode;
queue.push(neighbor);
// Observa se o vizinho que está sendo checado atualmente...
// é o nosso destino
if (neighbor === endNode) {
// Começa a reconstruir o caminho mais curto a partir do vértice...
// de chegada
const shortestPath = [endNode];
// Obtém o vértice atual de onde os vizinhos foram obtidos
let prevNode = currNode;
// Loop enquanto o caminho ainda não tiver sido reconstruído...
// até o ponto de partida
while (prevNode !== startNode) {
// Adiciona no começo da array `shortestPath` o vértice `prevNode`
shortestPath.unshift(prevNode);
// Obtém o predecessor do `prevNode` e faz dele o `prevNode` atual
prevNode = predecessor[prevNode];
}
shortestPath.unshift(startNode);
return shortestPath;
}
}
}
}
return null;
}
Ao executar o nosso código vemos o resultado da busca:
const connections = {
A: [ 'B', 'C' ],
B: [ 'A', 'D', 'F' ],
C: [ 'A', 'D', 'E' ],
D: [ 'B', 'C' ],
F: [ 'B', 'E' ],
E: [ 'C', 'F' ]
}
const shortestPath = findShortestPath(connections, 'A', 'F');
console.log(shortestPath); // ['A', 'B', 'F']
Podemos ver que o caminho mais curto do vértice ao vértice F de fato é A -> B -> F:
O algoritmo de busca em largura é uma ferramenta essencial na resolução de problemas que envolvem a descoberta do menor caminho entre dois pontos em um grafo. Mas é importante lembrar que cada aplicação pode ter suas particularidades e o algoritmo de pesquisa em largura não é o único e pode não ser o melhor algoritmo de busca pelo menor caminho em muitos casos.
Saber implementar um algoritmo de pesquisa em largura pode ajudar a solucionar problemas complexos em diversas áreas, como redes de transporte, otimização de rotas e até mesmo jogos.







Top comments (0)