Consistent hashing is a hashing technique that performs really well when operated in a dynamic environment where the distributed system scales up and scales down frequently. The core concept of Consistent Hashing was introduced in the paper Consistent Hashing and RandomTrees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web but it gained popularity after the famous paper introducing DynamoDB - Dynamo: Amazon’s Highly Available Key-value Store. Since then the consistent hashing gained traction and found a ton of use cases in designing and scaling distributed systems efficiently. The two famous examples that exhaustively use this technique are Bit Torrent, for their peer-to-peer networks and Akamai, for their web caches. In this article we dive deep into the need of Consistent Hashing, the internals of it, and more importantly along the way implement it using arrays and Binary Search.

Hash Functions

Before we jump into the core Consistent Hashing technique we first get a few things cleared up, one of which is Hash Functions. Hash Functions are any functions that map value from an arbitrarily sized domain to another fixed-sized domain, usually called the Hash Space. For example, mapping URLs to 32-bit integers or web pages' HTML content to a 256-byte string. The values generated as an output of these hash functions are typically used as keys to enable efficient lookups of the original entity.

An example of a simple hash function is a function that maps a 32-bit integer into an 8-bit integer hash space. The function could be implemented using the arithmetic operator modulo and we can achieve this by taking a modulo 256 which yields numbers in the range [0, 255] taking up 8-bits for its representation. A hash function, that maps keys to such integer domain, more often than not applies the modulo N so as to restrict the values, or the hash space, to a range [0, N-1].

A good hash function has the following properties

• The function is computationally efficient and the values generated are easy for lookups
• The function, for most general use cases, behaves like a pseudorandom generator that spreads data out evenly without any noticeable correlation

Now that we have seen what a hash function is, we take a look into how we could use them and build a somewhat scalable distributed system.

Building a distributed storage system

Say we are building a distributed storage system in which users can upload files and access them on demand. The service exposes the following APIs to the users

• upload to upload the file
• fetch to fetch the file and return its content

Behind the scenes the system has Storage Nodes on which the files are stored and accessed. These nodes expose the functions put_file and fetch_file that puts and gets the file content to/from the disk and sends the response to the main API server which in turn sends it back to the user.

To sustain the initial load, the system has 5 Stogare Nodes which stores the uploaded files in a distributed manner. Having multiple nodes ensures that the system, as a whole, is not overwhelmed, and the storage is distributed almost evenly across.

When the user invokes upload function with the path of the file, the system first needs to identify the storage node that will be responsible for holding the file and we do this by applying a hash function to the path and in turn getting the storage node index. Once we get the storage node, we read the content of the file and put that file on the node by invoking the put_file function of the node.

# storage_nodes holding instances of actual storage node objects
storage_nodes = [
    StorageNode(name='A', host='10.131.213.12'),
    StorageNode(name='B', host='10.131.217.11'),
    StorageNode(name='C', host='10.131.142.46'),
    StorageNode(name='D', host='10.131.114.17'),
    StorageNode(name='E', host='10.131.189.18'),
]


def hash_fn(key):
    """The function sums the bytes present in the `key` and then
    take a mod with 5. This hash function thus generates output
    in the range [0, 4].
    """
    return sum(bytearray(key.encode('utf-8'))) % 5


def upload(path):
    # we use the hash function to get the index of the storage node
    # that would hold the file
    index = hash_fn(path)

    # we get the StorageNode instance
    node = storage_nodes[index]

    # we put the file on the node and return
    return node.put_file(path)


def fetch(path):
    # we use the hash function to get the index of the storage node
    # that would hold the file
    index = hash_fn(path)

    # we get the StorageNode instance
    node = storage_nodes[index]

    # we fetch the file from the node and return
    return node.fetch_file(path)

The hash function used over here simply sums the bytes and takes the modulo by 5 (since there are 5 storage nodes in the system) and thus generating the output in the hash space [0, 4]. This output value now represents the index of the storage engine that will be responsible for holding the file.

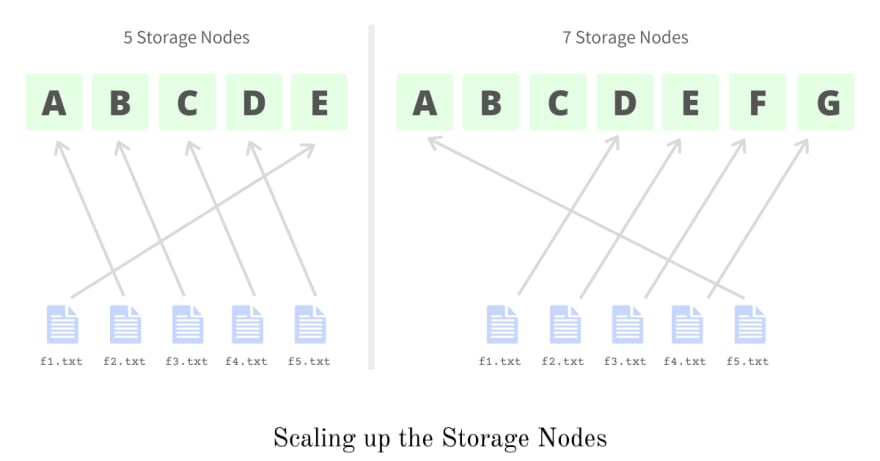
Say we have 5 files 'f1.txt', 'f2.txt', 'f3.txt', 'f4.txt', 'f5.txt' if we apply the hash function to these we find that they are stored on storage nodes E, A, B, C, and D respectively.

Things become interesting when the system gains some traction and it needs to be scaled to 7 nodes, which means now the hash function should do mod 7 instead of a mod 5. Changing the hash function implies changing the mapping and association of files with storage nodes. We first need to administer the new associations and see which files required to be moved from one node to another.

With the new hash function the same 5 files 'f1.txt', 'f2.txt', 'f3.txt', 'f4.txt', 'f5.txt' will now be associated with storage nodes D, E, F, G, A. Here we see that changing the hash function requires us to move every single one of the 5 files to a different node.

If we have to change the hash function every time we scale up or down and if this requires us to move not all but even half of the data, the process becomes super expensive and in longer run infeasible. So we need a way to minimize the data movement required during scale-ups or scale-downs, and this is where Consistent Hashing fits in and minimizes the required data transfer.

Consistent Hashing

The major pain point of the above system is that it is prone to events like scale-ups and scale-downs as it requires a lot of alterations in associations. These associations are purely driven by the underlying Hash Function and hence if we could somehow make this hash function independent of the number of the storage nodes in the system, we address this flaw.

Consistent Hashing addresses this situation by keeping the Hash Space huge and constant, somewhere in the order of [0, 2^128 - 1] and the storage node and objects both map to one of the slots in this huge Hash Space. Unlike in the traditional system where the file was associated with storage node at index where it got hashed to, in this system the chances of a collision between a file and a storage node are infinitesimally small and hence we need a different way to define this association.

Instead of using a collision-based approach we define the association as - the file will be associated with the storage node which is present to the immediate right of its hashed location. Defining association in this way helps us

• keep the hash function independent of the number of storage nodes
• keep associations relative and not driven by absolute collisions

Consistent Hashing on an average requires only k/n units of data to be migrated during scale up and down; where k is the total number of keys and n is the number of nodes in the system.

A very naive way to implement this is by allocating an array of size equal to the Hash Space and putting files and storage node literally in the array on the hashed location. In order to get association we iterate from the item's hashed location towards the right and find the first Storage Node. If we reach the end of the array and do not find any Storage Node we circle back to index 0 and continue the search. The approach is very easy to implement but suffers from the following limitations

• requires huge memory to hold such a large array
• finding association by iterating every time to the right is O(hash_space)

A better way of implementing this is by using two arrays: one to hold the Storage Nodes, called nodes and another one to hold the positions of the Storage Nodes in the hash space, called keys. There is a one-to-one correspondence between the two arrays - the Storage Node nodes[i] is present at position keys[i] in the hash space. Both the arrays are kept sorted as per the keys array.

Hash Function in Consistent Hashing

We define total_slots as the size of this entire hash space, typically of the order 2^256 and the hash function could be implemented by taking SHA-256 followed by a mod total_slots. Since the total_slots is huge and a constant the following hash function implementation is independent of the actual number of Storage Nodes present in the system and hence remains unaffected by events like scale-ups and scale-downs.

def hash_fn(key: str, total_slots: int) -> int:
    """hash_fn creates an integer equivalent of a SHA256 hash and
    takes a modulo with the total number of slots in hash space.
    """
    hsh = hashlib.sha256()

    # converting data into bytes and passing it to hash function
    hsh.update(bytes(key.encode('utf-8')))

    # converting the HEX digest into equivalent integer value
    return int(hsh.hexdigest(), 16) % total_slots

Adding a new node in the system

When there is a need to scale up and add a new node in the system, in our case a new Storage Node, we

• find the position of the node where it resides in the Hash Space
• populate the new node with data it is supposed to serve
• add the node in the Hash Space

When a new node is added in the system it only affects the files that hash at the location to the left and associated with the node to the right, of the position the new node will fit in. All other files and associations remain unaffected, thus minimizing the amount of data to be migrated and mapping required to be changed.

From the illustration above, we see when a new node K is added between nodes B and E, we change the associations of files present in the segment B-K and assign them to node K. The data belonging to the segment B-K could be found at node E to which they were previously associated with. Thus the only files affected and that needs migration are in the segment B-K; and their association changes from node E to node K.

In order to implement this at a low-level using nodes and keys array, we first get the position of the new node in the Hash Space using the hash function. We then find the index of the smallest key greater than the position in the sorted keys array using binary search. This index will be where the key and the new Storage node will be placed in keys and nodes array respectively.

def add_node(self, node: StorageNode) -> int:
    """add_node function adds a new node in the system and returns the key
    from the hash space where it was placed
    """

    # handling error when hash space is full.
    if len(self._keys) == self.total_slots:
        raise Exception("hash space is full")

    key = hash_fn(node.host, self.total_slots)

    # find the index where the key should be inserted in the keys array
    # this will be the index where the Storage Node will be added in the
    # nodes array.
    index = bisect(self._keys, key)

    # if we have already seen the key i.e. node already is present
    # for the same key, we raise Collision Exception
    if index > 0 and self._keys[index - 1] == key:
        raise Exception("collision occurred")

    # Perform data migration

    # insert the node_id and the key at the same `index` location.
    # this insertion will keep nodes and keys sorted w.r.t keys.
    self.nodes.insert(index, node)
    self._keys.insert(index, key)

    return key

Removing a new node from the system

When there is a need to scale down and remove an existing node from the system, we

• find the position of the node to be removed from the Hash Space
• populate the node to the right with data that was associated with the node to be removed
• remove the node from the Hash Space

When a node is removed from the system it only affects the files associated with the node itself. All other files and associations remain unaffected, thus minimizing the amount of data to be migrated and mapping required to be changed.

From the illustration above, we see when node K is removed from the system, we change the associations of files associated with node K to the node that lies to its immediate right i.e. node E. Thus the only files affected and needs migration are the ones associated with node K.

In order to implement this at a low-level using nodes and keys array, we get the index where the node K lies in the keys array using binary search. Once we have the index we remove the key from the keys array and Storage Node from the nodes array present on that index.

def remove_node(self, node: StorageNode) -> int:
    """remove_node removes the node and returns the key
    from the hash space on which the node was placed.
    """

    # handling error when space is empty
    if len(self._keys) == 0:
        raise Exception("hash space is empty")

    key = hash_fn(node.host, self.total_slots)

    # we find the index where the key would reside in the keys
    index = bisect_left(self._keys, key)

    # if key does not exist in the array we raise Exception
    if index >= len(self._keys) or self._keys[index] != key:
        raise Exception("node does not exist")

    # Perform data migration

    # now that all sanity checks are done we popping the
    # keys and nodes at the index and thus removing the presence of the node.
    self._keys.pop(index)
    self.nodes.pop(index)

    return key

Associating an item to a node

Now that we have seen how consistent hashing helps in keeping data migration, during scale-ups and scale-downs, to a bare minimum; it is time we see how to efficiently we can find the "node to the right" for a given item. The operation to find the association has to be super fast and efficient as it is something that will be invoked for every single read and write that happens on the system.

To implement this at low-level we again take leverage of binary search and perform this operation in O(log(n)). We first pass the item to the hash function and fetch the position where the item is hashed in the hash space. This position is then binary searched in the keys array to obtain the index of the first key which is greater than the position (obtained from the hash function). if there are no keys greater than the position, in the keys array, we circle back and return the 0th index. The index thus obtained will be the index of the storage node in the nodes array associated with the item.

def assign(self, item: str) -> str:
    """Given an item, the function returns the node it is associated with.
    """
    key = hash_fn(item, self.total_slots)

    # we find the first node to the right of this key
    # if bisect_right returns index which is out of bounds then
    # we circle back to the first in the array in a circular fashion.
    index = bisect_right(self._keys, key) % len(self._keys)

    # return the node present at the index
    return self.nodes[index]

The source code with the implementation of Consistent Hashing in Python could be found at github.com/arpitbbhayani/consistent-hashing.

Conclusion

Consistent Hashing is one of the most important algorithms to help us horizontally scale and manage any distributed system. The algorithm does not only work in sharded systems but also finds its application in load balancing, data partitioning, managing server-based sticky sessions, routing algorithms, and many more. A lot of databases owe their scale, performance, and ability to handle the humongous load to Consistent Hashing.

References

• Hash Functions - Wikipedia
• Consistent Hashing - Wikipedia
• Consistent Hashing - Stanford
• Consistent Hashing and RandomTrees
• Dynamo: Amazon’s Highly Available Key-value Store

Other articles you might like:

• Python Caches Integers
• Fractional Cascading - Speeding up Binary Searches
• Copy-on-Write Semantics
• What makes MySQL LRU cache scan resistant
• Building Finite State Machines with Python Coroutines

This article was originally published on my blog - Consistent Hashing.

If you liked what you read, subscribe to my newsletter and get the post delivered directly to your inbox and give me a shout-out @arpit_bhayani.