Strutture dati ad albero

Introduzione

Le reti blockchain utilizzano le transazioni per cambiare lo stato e tenere traccia dei saldi degli utenti, come abbiamo visto nella sezione precedente. Scaviamo ancora più a fondo nella complessità di questi sistemi e iniziamo a vedere quali strutture dati utilizzano per memorizzare tutti questi dati di stato in continua evoluzione.

Un orientamento agli alberi

Prima di tutto, gli informatici sono strani. A noi piace disegnare gli alberi al contrario lol

Come nella vita reale esistono molti tipi di alberi, anche in informatica esistono molte strutture di dati simili ad alberi. Vediamo di familiarizzare con alcuni di questi alberi.

Assicuratevi di dare un'occhiata ai termini in grassetto, poiché si tratta di un vocabolario molto importante da imparare per le blockchain in generale!

I nodi

Il primo termine che vedrete ampiamente utilizzato nelle strutture dati: nodi. Un nodo è un'unità di base di una struttura di dati.

Nei sistemi informatici, "nodo" può anche riferirsi ai nodi di rete che comunicano dati su una rete peer-to-peer (come sono Bitcoin ed Ethereum!). Il contesto è importante!

Albero semplice

Nel nodo semplice come nella foto qui sopra, vediamo un nodo arancione in alto, definito genitore, mentre i nodi verdi in basso vengono definiti figli (rispetto al nodo genitore).

Albero binario

E' tipico osservare qualche proprietà di applicazione delle strutture "albero" per distinguerne i diversi tipi di dati.

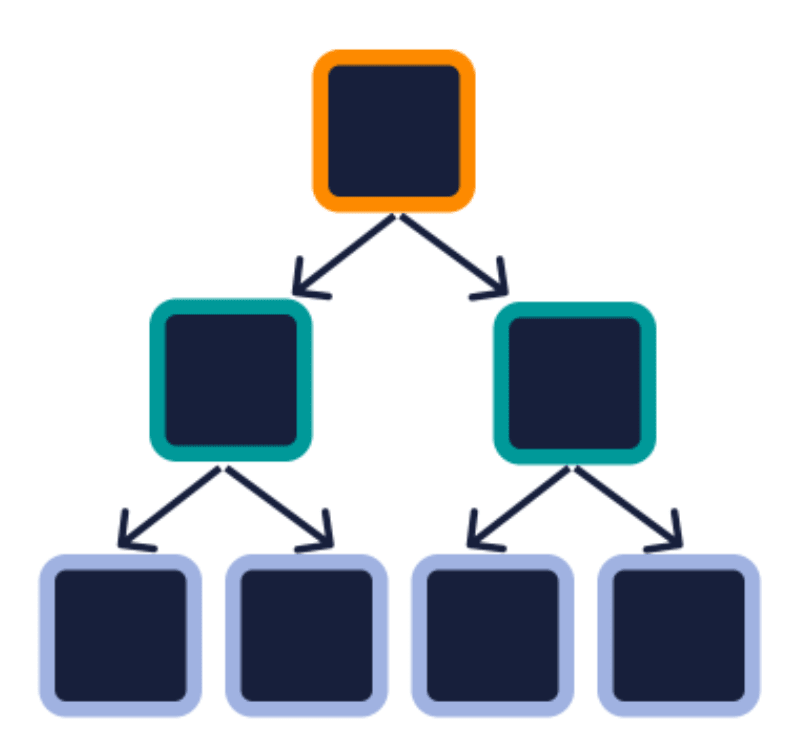
Un albero è considerato binario quando ogni genitore ha al massimo due figli. La parola chiave di questo albero è "binario" che, come altri termini che precedono "albero", stabilisce un tipo di regola per l'albero, in questo caso che ogni nodo genitore può avere al massimo due figli.

Si noti che l'albero nel diagramma precedente ha ora quattro nuovi nodi grigi. Questi vengono ora chiamati foglie, poiché sono l'ultimo livello dell'albero e non hanno altri figli.

Un albero generico

L'albero qui sopra mostra che un albero può essere un genitore qualsiasi con un numero qualsiasi di figli. Non è necessario che l'albero sia sottoposto a regole, è semplicemente un albero di dati.

Vedremo emergere uno schema in cui la parola "albero" è solitamente preceduta da un termine che indica quali tipi di regole l'albero applicherà. Un albero binario applica la regola secondo cui i genitori possono avere al massimo due figli. Un albero senza aggettivi... beh è solo un albero!

Albero vs. Elenco collegato

Anche un elenco collegato è un albero, solo che è molto lungo e ha solo un figlio per ogni genitore in una lunga catena continua. Un albero non è necessariamente un elenco collegato. Ecco le due implementazioni del codice per un LinkedListNode e unTreeNode, per aiutare a distinguere:

class LinkedListNode {
    constructor(data) {
        this.data = data;
        this.next = null;
    }
}

class TreeNode {
    constructor(data) {
        this.data = data;
        this.children = []; // riferimento al figlio 
    }
}

Si noti che il TreeNode contiene i dati tipici e un array per contenere i riferimenti ai figli di quel nodo (genitore).

Il LinkedListNode tiene solo traccia di un nodo successivo.

Vocaboli utili

Notate tutte le relatività che si verificano quando un albero cresce di dimensioni. Un nodo che era un nodo foglia diventa un nodo genitore una volta aggiunto un nuovo figlio sotto di esso.

Ecco alcuni vocaboli utili quando si parla di strutture dati ad albero:

• chiave (key): dati effettivi contenuti nel nodo;
• radice (root): il nodo padre di un albero;
• fratelli (siblings): nodi sotto lo stesso genitore e allo stesso livello;
• sottoalbero (subtree): una volta isolata una parte di un albero più ampio, è possibile formare un albero nuovo con nuove relazioni;

Quando usare un albero 🌲

A volte gli alberi si formano in modo del tutto naturale! LOL
Prendiamo ad esempio un file system:

Un file system ad esempio può essere un albero con una quantità arbitraria di figli in ogni directory.

Uso dell'albero:

Se i dati possono essere memorizzati in modo gerarchico, l'uso di un albero può essere una buona struttura di dati da utilizzare.
Un albero è anche una struttura dati molto efficiente per la ricerca e l'ordinamento dei dati.
Gli algoritmi ricorsivi sono spesso utilizzati insieme agli alberi.
Questi ultimi infatti possono essere strutture di dati molto efficienti per la ricerca e l'ordinamento dei dati proprio per le regole che stabiliscono, come abbiamo visto per l'albero binario, o addirittura un insieme di regole ancora più rigide, come con l'albero di ricerca binario.

Albero di ricerca binario

Un albero di ricerca binario, come quello sopra descritto, ha le seguenti proprietà:

• è un albero binario;
• il sottoalbero sinistro di un nodo contiene solo nodi con chiavi minori della chiave del nodo stesso;
• il sottoalbero destro di un nodo contiene solo nodi con chiavi maggiori della chiave del nodo stesso;
• anche i sottoalberi sinistro e destro di ogni nodo devono essere un albero di ricerca binario;

Questi tipi di imposizioni rendono l'albero di ricerca binario una struttura dati molto richiesta, poiché gli algoritmi possono ora tenere conto di queste regole e la memorizzazione/ricerca è molto più efficiente;

Curiosità sull'albero di ricerca binario

Sapendo che ogni figlio sinistro è minore del genitore e ogni figlio destro è maggiore del genitore, quanti tentativi sono necessari per trovare un numero (chiave) al massimo?

L'aggiunta di un nuovo livello di elementi aggiunge solo 1 tentativo di ricerca in più, nella peggiore delle ipotesi. Grazie alle proprietà di applicazione del BST (acronimo di Binary Search Tree), il tempo di ricerca rimane sempre O(log n), dove n è il numero di nodi dell'albero.

L'albero nel diagramma qui sopra è un BST di altezza (quanti livelli ha un albero) pari a tre, con nodi a ogni livello che aumentano di una potenza di due a ogni livello inferiore. L'ultimo livello contiene 4 nodi, il che significa che il livello successivo conterrà 8 nodi (al massimo). Ecco la vera magia degli alberi a proprietà forzata come i BST: anche se aggiungiamo un intero nuovo livello di nuovi dati, il tempo di ricerca aumenta solo di uno. In altre parole, mentre la dimensione dell'albero cresce in modo esponenziale, il tempo di ricerca rimane sempre O(log n).

Ecco un grafico per visualizzare quanto il tempo di ricerca dell'algoritmo sia influenzato dalla crescita dell'input (n).

Poiché le blockchain sono fondamentalmente dei database, la notazione O-Grande è molto importante per aiutare a scegliere la struttura dei dati più efficiente (bassi costi di archiviazione, facilità di ricerca e recupero).
Quando si progetta un sistema con esigenze di dati, si desidera che la struttura dei dati sia il più possibile vicina al tempo costante (la linea blu del grafico).

La notazione O-Grande ci dà un indicatore approssimativo del rendimento di un algoritmo in termini di N (numero di elementi in ingresso). Vogliamo che i nostri algoritmi siano efficienti.

Conclusione

Abbiamo trattato le strutture dati ad albero di base, i diversi tipi di applicazione sugli alberi e il vocabolario generale delle strutture dati ad albero. Si tratta di informazioni importanti per addentrarci ancora di più in alberi più specifici e con imposizioni più specifiche. Nel prossimo post invece, affronteremo gli alberi di Merkle.