Regularização é um tema importante quando o assunto é uma boa modelagem mas antes de entrarmos no assunto precisamos entender o conceito de viés e variância. Eles são o propósito do uso das regularizações.
Viés e Variância
A incapacidade de um modelo de capturar a verdadeira relação entre variáveis e o objeto a ser predito é o que chamamos de VIÉS (Bias em inglês).
Então, quando o erro de viés é alto significa que o modelo não está aprendendo nada.
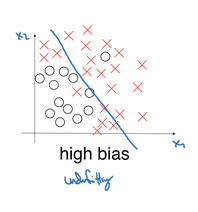
Nessa imagem temos a linha azul como sendo o nosso modelo onde queremos separar esse dataset em duas categoriais. Veja que há muitos X vermelhos juntos com as bolinhas, as categorias não foram muito bem separadas, isso significa que o modelo ainda não entendeu a “curva” que ele deveria fazer para categorizar esses dados corretamente. Chamamos isso de Underfitting.
Por outro lado, se há um viés muito pequeno o modelo fica tão ajustado aos dados de treinamento que quando é usado com dados diferentes acaba errando muito. Aqui entra o conceito de variância.
A variância é a sensibilidade de um modelo ao ser usado com outros datasets diferentes do treinamento. Se o modelo é muito sensível aos dados de treinamento, ou seja, identificou tão bem a relação entre os dados de treinamento, que quando colocado em teste irá errar justamente a variação que existe entre os datasets.
Veja na última imagem como o nosso modelo está acertando absolutamente todos os dados. Chamamos isso de Overfitting. O modelo ideal seria algo parecido com o modelo do meio da próxima imagem, gerando uma curva mais generalizada.
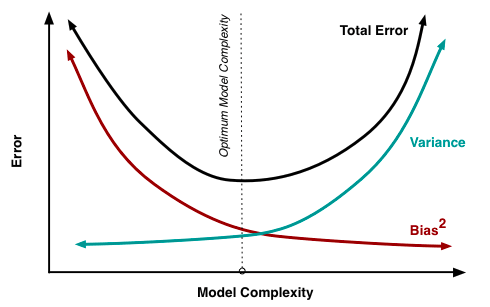
Agora observem a imagem abaixo, nela está representado o Trade-off. Percebam que o erro total do modelo é soma do viés (bias) com a variância e que conforme o modelo vai “aprendendo” (model complexity aumenta) temos um momento de baixa e logo depois o erro volta a crescer.
É muito comum modelos que aprendem muito bem no conjunto de treino, mas acabam apresentando Overfitting. Isso faz com que o modelo esteja do lado direito desse diagrama, entretanto, o ideal é que fique mais próximo ao meio. Então para diminuir a variância acrescentamos um pouquinhos de viés, assim ele “desaprende” o suficiente para conseguir generalizar e ser usado além dos dados de treino.
REGULARIZAÇÕES
A regularização introduz um RUÍDO no modelo para diminuir o erro de variância.
As regularizações que veremos também são chamadas de Regressões penalizadas. Regressões são modelos estatísticos inferenciais que tem como objetivo minimizar a soma dos resíduos ao quadrado (leia mais sobre regressões aqui). Abaixo temos o exemplo de uma Regressão Linear Simples, onde os dados vermelhos seriam o nosso conjunto de treino. A reta dessa Regressão foi escolhida por ser a que possui a menor soma dos resíduos ao quadrado de acordo com a sua base de treino, mas isso não fez com que essa fosse a melhor reta contando com todos os outros pontos.
Nas Regularizações o objetivo não é minimizar apenas a soma dos resíduos ao quadrado (SRQ) mas também um valor penalizado em cima dos parâmetros da regressão.
Ridge Regression
Nessa vamos minimizar a soma dos resíduos ao quadrado + uma penalização em cima de todos os parâmetros ao quadrado. A função a ser minimizada pela regressão ficaria (onde λ é um número utilizado para penalização):
SRQ + λ * ( parâmetro₁² + parâmetro₂² + …)
Agora podemos observar a diferença nas retas de uma Regressão Simples e uma Regularização. Veja que, apesar da reta não estar totalmente ajustada aos dados de treino, o seu ajuste ao total dos dados melhorou.
As regularizações funcionam de forma muito parecida mas não servem apenas para evitar o overfitting. Isso é o que podemos ver mais claramente na Lasso Regression.
Lasso Regression
A Lasso também penaliza os parâmetros, entretanto, ao invés de colocá-los ao quadrado, eles são usados em módulo. A função minimizada então seria essa:
SRQ + λ * ( |parâmetro₁| + |parâmetro₂| + …)
Beleza, mas e daí?
A grande diferença entre Lasso e Rigde é que a Lasso pode levar os parâmetros a (exatamente) 0 enquanto a Ridge apenas próximo à 0.
Isso significa que:
Parâmetros ruins usados na modelagem podem ser EXCLUÍDOS da equação. Ou seja, Regularizações também podem ser úteis na escolha dos parâmetros para as nossas modelagens.
Ridge Regression seria bem utilizada quando sabemos que a maioria dos parâmetros são úteis para o modelo. Já uma Lasso Regression quando temos muitos parâmetros e alguns deles podem ser inúteis. Além das duas, ainda temos mais um tipo de regressão penalizada que combina as duas últimas.
Elastic-Net Regression
Elastic-Net é uma combinação da penalização da Lasso e Ridge. Sua função de minimização fica como mostrado abaixo:
SRQ +
λ₁ * ( |parâmetro₁| + |parâmetro₂| + …) +
λ₂ * ( parâmetro₁² + parâmetro₂² + …)
Lasso + Ridge
Essa técnica ainda é boa para quando há parâmetros correlacionados. Já que no Lasso a maioria deles seria excluída e no Ridge esses parâmetros apenas teriam valores muito baixo.
Referências
Algumas referências que usei para aprender sobre o assunto do post :D :
Regularization Tutorial — DataCamp







Top comments (0)