Insertion Sort is a comparison-based sorting algorithm that works by iteratively building a sorted portion of the array or list, one element at a time. It starts with the assumption that the first element is already sorted. Then, it considers the next element and inserts it into the correct position in the sorted portion, shifting other elements as necessary. This process is repeated until the entire array is sorted.
How Insertion Sort Works
Insertion Sort works by iteratively building a sorted portion of the array or list, one element at a time. It starts with the assumption that the first element is already sorted. Then, it considers the next element and inserts it into the correct position in the sorted portion, shifting other elements as necessary. This process is repeated until the entire array is sorted.
Here are the step-by-step operations of Insertion Sort on this array:
Step 1: Start with the second element (2) and compare it with the element in the sorted portion (5). Since 2 is smaller, we shift 5 to the right and insert 2 at the first position: [2, 5, 8, 12, 1].
Step 2: Move to the third element (8) and compare it with the elements in the sorted portion (2, 5). Since 8 is larger, we leave it at its position: [2, 5, 8, 12, 1].
Step 3: Repeat step 2 for the fourth element (12). Since 12 is larger than all the elements in the sorted portion, it remains in its position: [2, 5, 8, 12, 1].
Step 4: Finally, consider the fifth element (1) and compare it with the elements in the sorted portion (2, 5, 8, 12). Since 1 is smaller, we shift all the larger elements to the right and insert 1 at the first position: [1, 2, 5, 8, 12].
After these steps, the array is sorted in ascending order.
Implementation Steps
Step 1: Prompt the user to enter the size of the array by using the input() function and convert it to an integer using the int() function. Store the value in a variable named n.
Step 2: Create an empty list called arr to store the elements of the array.
Step 3: Use a for loop to iterate n times. Inside the loop, prompt the user to enter each element of the array using the input() function, convert it to an integer, and append it to the arr list.
Step 4: Use a for loop to iterate over the range from 1 to n.
Step 5: Inside the loop, store the current element in a variable named current.
Step 6: Create a variable named j and set it equal to i - 1.
Step 7: Use a while loop to compare the element at index j with the current element. If the element at index j is greater than the current element and j is greater than or equal to 0, shift the element at index j to the right by assigning the value of arr[j] to arr[j + 1]. Decrement j by 1.
Step 8: After the while loop completes, insert the current element at the correct position by assigning its value to arr[j + 1].
Step 9: After the outer for loop completes, use another for loop to iterate over the arr list and print each element, separated by a space, using the print() function with the end parameter set to " ".
Code
n=int(input("Enter size of array: "))
arr = []
for i in range(n):
arr.append(int(input()))
print('Unsorted Array: ')
for i in arr:
print(i, end=" ")
for i in range(1, n):
current = arr[i]
j = i-1
while(arr[j]>current and j>=0):
arr[j+1] = arr[j]
j-=1
arr[j+1] = current
print('Sorted Array: ')
for i in arr:
print(i, end=" ")
Example
Enter the size of the array: 5
8
5
6
2
7
Unsorted Array: 8 5 6 2 7
Sorted Array: 2 5 6 7 8
Time Complexity
The time complexity of Insertion Sort is O(n^2) in the worst case and average case. In the best case scenario, when the array is already sorted, the time complexity is O(n).
Conclusion
Insertion Sort is a simple yet efficient sorting algorithm that is particularly useful for small datasets or partially sorted arrays. Its simplicity, in-place sorting capability, and average-case time complexity of O(n) make it a valuable tool for programmers. However, it may not be the best choice for large datasets or arrays that are already mostly sorted.


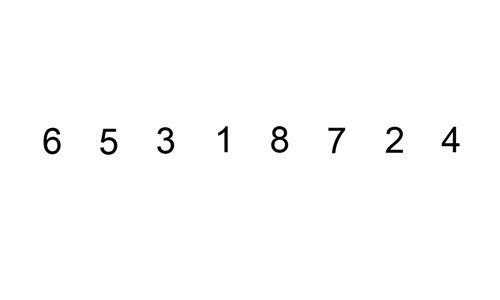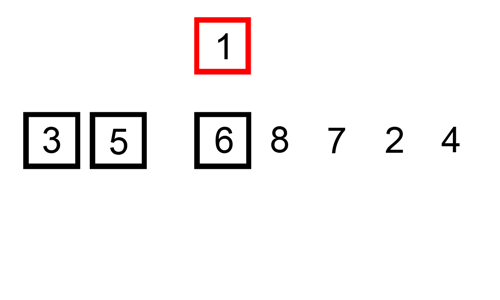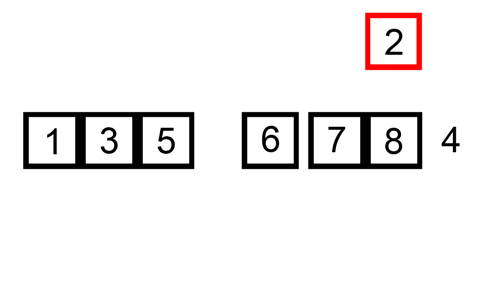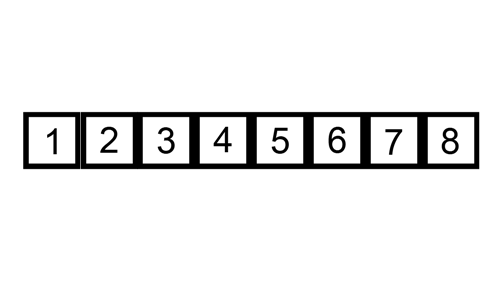





Top comments (0)