I’ve been publishing screencasts demonstrating how to use the tidymodels framework, from first steps in modeling to how to tune more complex models. Today, I’m using this week’s #TidyTuesday dataset on beer production to show how to use bootstrap resampling to estimate model parameters.
Here is the code I used in the video, for those who prefer reading instead of or in addition to video.
Explore the data
Our modeling goal here is to estimate how much sugar beer producers use relative to malt according to the #TidyTuesday dataset. We’ll use bootstrap resampling to do this! 🍻
First, let’s look at the data on brewing materials.
library(tidyverse)
brewing_materials_raw <- read_csv("https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2020/2020-03-31/brewing_materials.csv")
brewing_materials_raw %>%
count(type, wt = month_current, sort = TRUE)
## # A tibble: 12 x 2
## type n
## <chr> <dbl>
## 1 Total Used 53559516695
## 2 Total Grain products 44734903124
## 3 Malt and malt products 32697313882
## 4 Total Non-Grain products 8824613571
## 5 Sugar and syrups 6653104081
## 6 Rice and rice products 5685742541
## 7 Corn and corn products 5207759409
## 8 Hops (dry) 1138840132
## 9 Other 998968470
## 10 Barley and barley products 941444745
## 11 Wheat and wheat products 202642547
## 12 Hops (used as extracts) 33700888
How have some different brewing materials changed over time?
brewing_filtered <- brewing_materials_raw %>%
filter(
type %in% c(
"Malt and malt products",
"Sugar and syrups",
"Hops (dry)"
),
year < 2016,
!(month == 12 & year %in% 2014:2015)
) %>%
mutate(
date = paste0(year, "-", month, "-01"),
date = lubridate::ymd(date)
)
brewing_filtered %>%
ggplot(aes(date, month_current, color = type)) +
geom_point()
There are strong annual patterns in these materials. We want to measure how much sugar beer producers use relative to malt.
brewing_materials <- brewing_filtered %>%
select(date, type, month_current) %>%
pivot_wider(
names_from = type,
values_from = month_current
) %>%
janitor::clean_names()
brewing_materials
## # A tibble: 94 x 4
## date malt_and_malt_products sugar_and_syrups hops_dry
## <date> <dbl> <dbl> <dbl>
## 1 2008-01-01 374165152 78358212 4506546
## 2 2008-02-01 355687578 80188744 1815271
## 3 2008-03-01 399855819 78907213 6067167
## 4 2008-04-01 388639443 81199989 6864440
## 5 2008-05-01 411307544 89946309 7470130
## 6 2008-06-01 415161326 81012422 7361941
## 7 2008-07-01 405393784 76728131 1759452
## 8 2008-08-01 389391266 83928121 5992025
## 9 2008-09-01 362587470 71982604 3788942
## 10 2008-10-01 353803777 42828943 3788949
## # … with 84 more rows
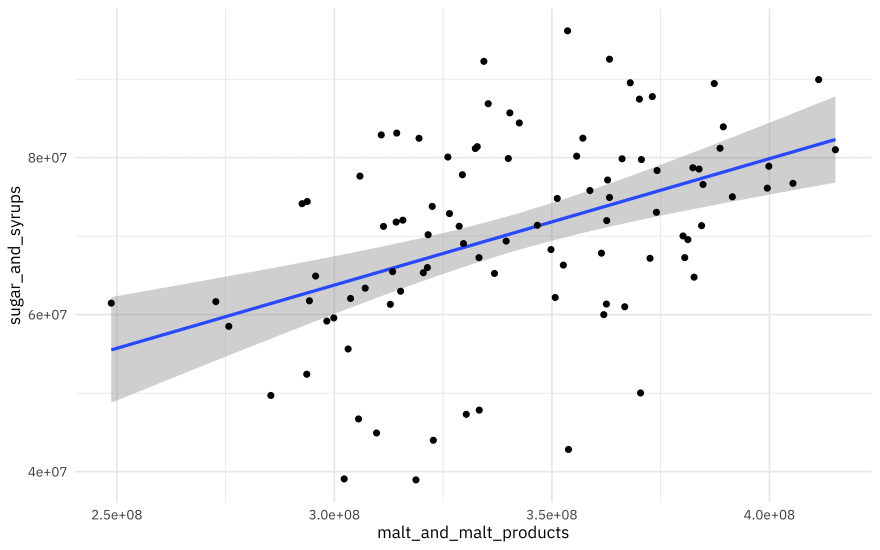
brewing_materials %>%
ggplot(aes(malt_and_malt_products, sugar_and_syrups)) +
geom_smooth(method = "lm") +
geom_point()
There is a lot of variation in this relationship, but beer reproducers use more sugar when they use more malt. What is the relationship?
library(tidymodels)
beer_fit <- lm(sugar_and_syrups ~ 0 + malt_and_malt_products,
data = brewing_materials
)
summary(beer_fit)
##
## Call:
## lm(formula = sugar_and_syrups ~ 0 + malt_and_malt_products, data = brewing_materials)
##
## Residuals:
## Min 1Q Median 3Q Max
## -29985291 -6468052 174001 7364462 23462837
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## malt_and_malt_products 0.205804 0.003446 59.72 <2e-16 ***
## ---
## Signif. codes: 0 ' ***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11480000 on 93 degrees of freedom
## Multiple R-squared: 0.9746, Adjusted R-squared: 0.9743
## F-statistic: 3567 on 1 and 93 DF, p-value: < 2.2e-16
tidy(beer_fit)
## # A tibble: 1 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 malt_and_malt_products 0.206 0.00345 59.7 5.72e-76
Here I am choosing to set the intercept to zero to take a simplified view of the malt-sugar relationship (i.e., beer producers don’t use any sugar if they aren’t starting with malt). We could leave that off and estimate both an intercept (baseline use of sugar all the time) and slope (increase in use of sugar per barrel of malt).
This model and the visualization above are based on model assumptions that may not hold with our real-world beer production data. Bootstrap resampling provides predictions and confidence intervals that are more robust.
Bootstrap resampling
First, let’s create a set of bootstrap resamples.
set.seed(123)
beer_boot <- bootstraps(brewing_materials, times = 1e3, apparent = TRUE)
beer_boot
## # Bootstrap sampling with apparent sample
## # A tibble: 1,001 x 2
## splits id
## <list> <chr>
## 1 <split [94/39]> Bootstrap0001
## 2 <split [94/34]> Bootstrap0002
## 3 <split [94/37]> Bootstrap0003
## 4 <split [94/39]> Bootstrap0004
## 5 <split [94/29]> Bootstrap0005
## 6 <split [94/27]> Bootstrap0006
## 7 <split [94/35]> Bootstrap0007
## 8 <split [94/33]> Bootstrap0008
## 9 <split [94/29]> Bootstrap0009
## 10 <split [94/34]> Bootstrap0010
## # … with 991 more rows
Next, let’s train a model to each of these bootstrap resamples. We can use tidy() with map() to create a dataframe of model results.
beer_models <- beer_boot %>%
mutate(
model = map(splits, ~ lm(sugar_and_syrups ~ 0 + malt_and_malt_products, data = .)),
coef_info = map(model, tidy)
)
beer_coefs <- beer_models %>%
unnest(coef_info)
beer_coefs
## # A tibble: 1,001 x 8
## splits id model term estimate std.error statistic p.value
## <list> <chr> <lis> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 <split [9… Bootstra… <lm> malt_and_ma… 0.203 0.00326 62.3 1.31e-77
## 2 <split [9… Bootstra… <lm> malt_and_ma… 0.208 0.00338 61.7 3.17e-77
## 3 <split [9… Bootstra… <lm> malt_and_ma… 0.205 0.00336 61.1 7.30e-77
## 4 <split [9… Bootstra… <lm> malt_and_ma… 0.206 0.00361 57.1 3.26e-74
## 5 <split [9… Bootstra… <lm> malt_and_ma… 0.203 0.00349 58.3 4.77e-75
## 6 <split [9… Bootstra… <lm> malt_and_ma… 0.209 0.00335 62.2 1.33e-77
## 7 <split [9… Bootstra… <lm> malt_and_ma… 0.210 0.00330 63.7 1.73e-78
## 8 <split [9… Bootstra… <lm> malt_and_ma… 0.209 0.00359 58.2 5.52e-75
## 9 <split [9… Bootstra… <lm> malt_and_ma… 0.207 0.00342 60.5 1.74e-76
## 10 <split [9… Bootstra… <lm> malt_and_ma… 0.207 0.00378 54.9 1.14e-72
## # … with 991 more rows
Evaluate results
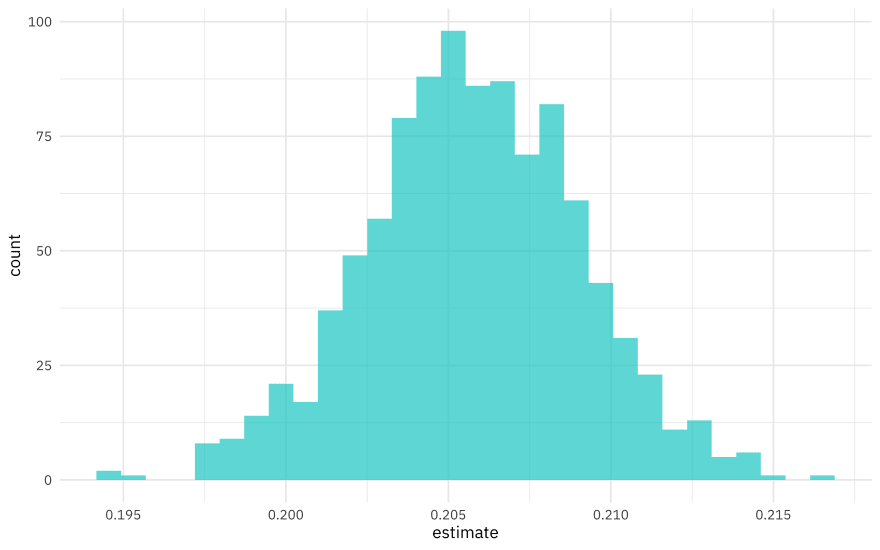
What is the distribution of the relationship between sugar and malt?
beer_coefs %>%
ggplot(aes(estimate)) +
geom_histogram(alpha = 0.7, fill = "cyan3")
We can see where this distribution is centered and how broad it is from this visualization, and we can estimate these quantities using int_pctl() from the rsample package.
int_pctl(beer_models, coef_info)
## # A tibble: 1 x 6
## term .lower .estimate .upper .alpha .method
## <chr> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 malt_and_malt_products 0.199 0.206 0.212 0.05 percentile
We can also visualize some of these fits to the bootstrap resamples. First, let’s use augment() to get the fitted values for each resampled data point.
beer_aug <- beer_models %>%
sample_n(200) %>%
mutate(augmented = map(model, augment)) %>%
unnest(augmented)
beer_aug
## # A tibble: 18,800 x 13
## splits id model coef_info sugar_and_syrups malt_and_malt_p… .fitted
## <list> <chr> <lis> <list> <dbl> <dbl> <dbl>
## 1 <spli… Boot… <lm> <tibble … 71341108 384396702 7.78e7
## 2 <spli… Boot… <lm> <tibble … 76728131 405393784 8.20e7
## 3 <spli… Boot… <lm> <tibble … 73793509 322480722 6.53e7
## 4 <spli… Boot… <lm> <tibble … 85703037 340319408 6.89e7
## 5 <spli… Boot… <lm> <tibble … 67266337 380521275 7.70e7
## 6 <spli… Boot… <lm> <tibble … 81199989 388639443 7.86e7
## 7 <spli… Boot… <lm> <tibble … 76115769 399504457 8.08e7
## 8 <spli… Boot… <lm> <tibble … 66002563 321371392 6.50e7
## 9 <spli… Boot… <lm> <tibble … 85703037 340319408 6.89e7
## 10 <spli… Boot… <lm> <tibble … 74805384 351222725 7.11e7
## # … with 18,790 more rows, and 6 more variables: .se.fit <dbl>, .resid <dbl>,
## # .hat <dbl>, .sigma <dbl>, .cooksd <dbl>, .std.resid <dbl>
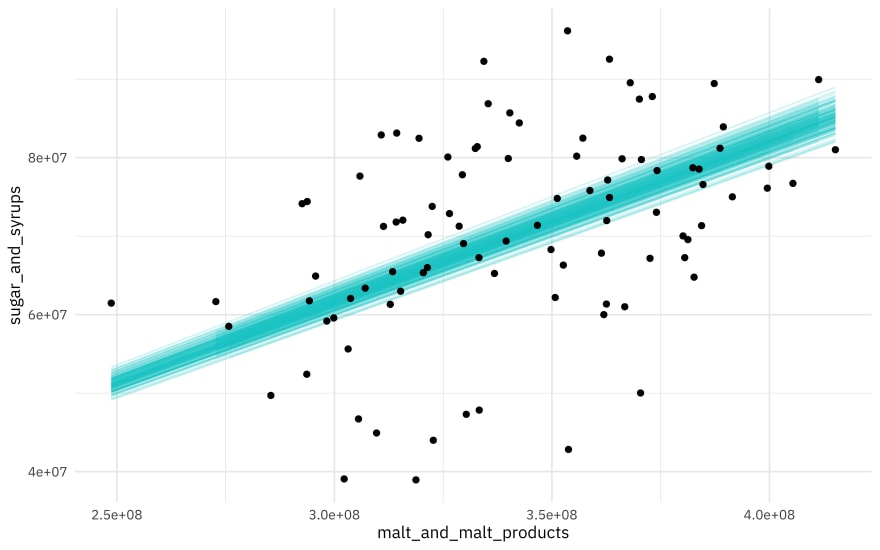
Then, let’s create a visualization.
ggplot(beer_aug, aes(malt_and_malt_products, sugar_and_syrups)) +
geom_line(aes(y = .fitted, group = id), alpha = .2, col = "cyan3") +
geom_point()







Top comments (0)