This is a translation of Functors, Applicatives, And Monads In Pictures from Haskell into ReasonML.
I take no credit for this work, and if you enjoy this post be sure to say thanks to Aditya Bhargava (@_egonschiele) the author of the original version.
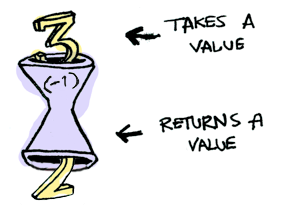
Here's a simple value:
And we know how to apply a function to this value:
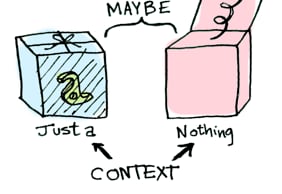
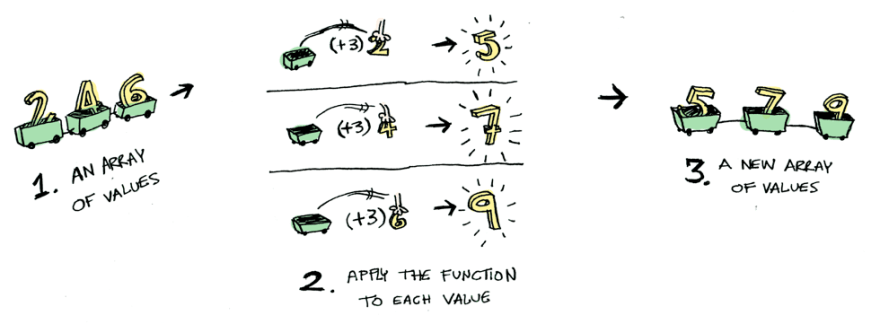
Simple enough. Let's extend this by saying that any value can be in a context. For now you can think of a context as a box that you can put a value in:
Now when you apply a function to this value, you'll get different results depending on the context. This is the idea that Functors, Applicatives, Monads, Arrows etc are all based on.
Let's create a Maybe data type that defines two related contexts:
module Maybe = {
type t('a) =
| Nothing
| Just('a);
}
In a second we'll see how function application is different when something is a Just(a) versus a Nothing. First let's talk about Functors!
Functors
When a value is wrapped in a context, you can't apply a normal function to it:
This is where fmap comes in. fmap is from the street, fmap is hip to contexts. fmap knows how to apply functions to values that are wrapped in a context.
Suppose you want to apply (+3) to Just(2). We can implement fmap:
Maybe.fmap((+)(3), Just(2));
// Just(5)
Bam! fmap shows us how it's done!
Just what is a Functor, really?
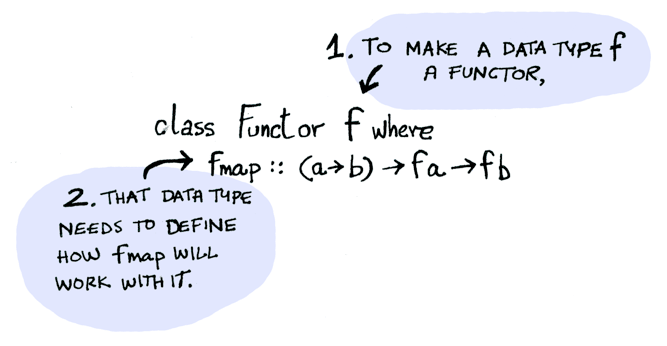
Functor is a class of functions that define an fmap function.
In Haskell they are defined as a type class.
In ReasonML we don't have type classes yet, but they are being worked on in OCaml, and therefore ReasonML.
Here's the definition:
A Functor is any data type that defines how fmap applies to it. Here's how fmap works:
So we can do this:
Maybe.fmap((+)(3), Just(2));
// Just(5)
This specifies how fmap applies to Justs and Nothings:
Let's add fmap to our Maybe module:
let fmap = (f, m) => {
switch (m) {
| Nothing => Nothing
| Just(a) => Just(f(a))
};
};
Here's what is happening behind the scenes when we write Maybe.fmap((+)(3), Just(2));:
So then you're like, alright fmap, please apply (+3) to a Nothing?
Maybe.fmap((+)(3), Nothing)
// Nothing
Like Morpheus in the Matrix, fmap knows just what to do; you start with Nothing, and you end up with Nothing! fmap is zen. Now it makes sense why the Maybe data type exists. For example, here's how you work with a database record in a language without Maybe:
post = Post.find_by_id(1)
if post
return post.title
else
return nil
end
Let's create a simple Post module in ReasonML with these functions.
module Post = {
type t = {
id: int,
title: "string,"
};
let make = (id, title) => {id, title};
let fmap = (f, post) => f(post);
let getPostTitle = post => post.title;
let findPost = id => make(id, "Post #" ++ string_of_int(id));
};
Now we can write:
Post.(fmap(getPostTitle, findPost(1)));
If findPost returns a post, we will get the title with getPostTitle. If it returns Nothing, we will return Nothing! Pretty neat, huh?
In Haskell, <$> is the common infix version of fmap.
In ReasonML we can create an equivalent alias. Adding to our Post module:
let (<$>) = fmap;
So we can now write:
Post.(getPostTitle <$> findPost(1));
Here's another example: what happens when you apply a function to a list?
Lists can operate as functors too!
In ReasonML we can make use of the list map function:
List.map
Okay, okay, one last example: what happens when you apply a function to another function?
For this case we can define a Function module that has fmap:
module Function = {
let fmap = (f, g, x) => f(g(x));
};
So we can now write:
Function.fmap((+)(3), (+)(1));
Here's a function:
Here's a function applied to another function:
The result is just another function!
let foo = Function.fmap((+)(3), (+)(2));
foo(10);
// 15
So functions can be Functors too!
When you use fmap on a function, you're just doing function composition!
Applicatives
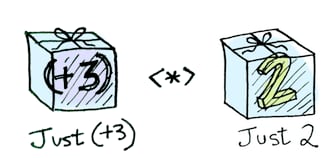
Applicatives take it to the next level. With an applicative, our values are wrapped in a context, just like Functors:
But our functions are wrapped in a context too!
Yeah. Let that sink in. Applicatives don't kid around. They know how to apply a function wrapped in a context to a value wrapped in a context:
Applicatives define an apply function, also written as <*> in Haskell, which we can create an alias for in ReasonML.
Let's add the applicative functions to our Maybe module:
let apply = (mf, mv) => {
switch (mv) {
| Nothing => Nothing
| Just(v) =>
switch (mf) {
| Nothing => Nothing
| Just(f) => Just(f(v))
}
};
};
let (<*>) = apply;
Here's an example using them:
Maybe.(Just((+)(3)) <*> Just(2));
// Just(5)
Let's also define applicative functions for a list. We'll create a MyList module to avoid name clashes with the built in List module:
module MyList = {
type apply('a, 'b) = (list('a => 'b), list('a)) => list('b);
let apply: apply('a, 'b) =
(fs, xs) => List.flatten(List.map(f => List.map(f, xs), fs));
let (<*>) = apply;
};
Using <*> can lead to some interesting situations. For example:
let funList = [(*)(2), (+)(3)];
let valList = [1, 2, 3];
MyList.(funList <*> valList);
// [2, 4, 6, 4, 5, 6]
Here's something you can do with Applicatives that you can't do with Functors. How do you apply a function that takes two arguments to two wrapped values?
Maybe.((+) <$> Just(5));
// Just((+)(5))
Maybe.(Just((+)(5)) <$> Just(4));
// ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST
Applicatives:
Maybe.((+) <$> Just(5));
// Just((+)(5))
Maybe.(Just((+)(5)) <*> Just(3));
// Just(8)
Applicative pushes Functor aside. "Big boys can use functions with any number of arguments," it says. "Armed with <$> and <*>, I can take any function that expects any number of unwrapped values. Then I pass it all wrapped values, and I get a wrapped value out! AHAHAHAHAH!"
Maybe.((*) <$> Just(5) <*> Just(3));
Monads
How to learn about Monads:
- Get a PhD in computer science.
- Throw it away because you don't need it for this section!
Monads add a new twist.
Functors apply a function to a wrapped value:
Applicatives apply a wrapped function to a wrapped value:
Monads apply a function that returns a wrapped value to a wrapped value.
Monads have a function bind, or the operator alias >>= to do this.
Let's see an example.
First, we'll need to add bind to our good ol' Maybe module:
let bind = (mv, f) => {
switch (mv) {
| Nothing => Nothing
| Just(v) => f(v)
};
};
let (>>=) = bind;
Suppose half is a function that only works on even numbers:
Let's write half in ReasonML (we'll also need to define even and odd functions):
/*
Mutually recursive function
https://ocaml.org/learn/tutorials/labels.html
*/
let rec even = x =>
if (x <= 0) {
true;
} else {
odd(x - 1);
}
and odd = x =>
if (x <= 0) {
false;
} else {
even(x - 1);
};
let half = x =>
if (even(x)) {
Maybe.Just(x / 2);
} else {
Nothing;
};
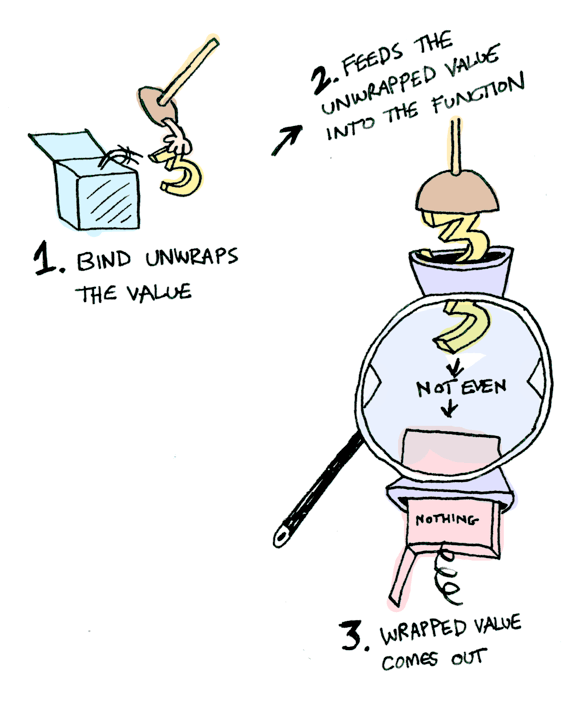
What if we feed it a wrapped value?
We need to use >>= to shove our wrapped value into the function. Here's a photo of >>=:
Here's how it works:
Maybe.(Just(3) >>= half);
// Nothing
Maybe.(Just(4) >>= half);
// Just(2)
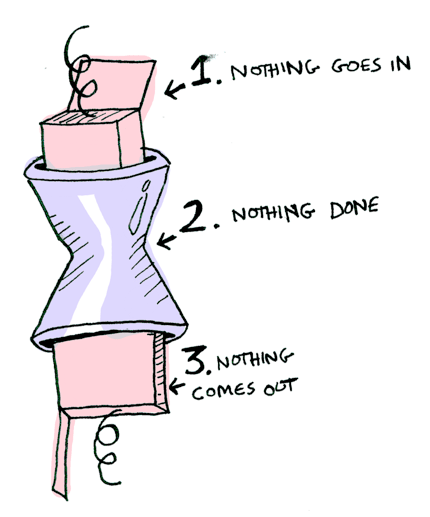
Maybe.(Nothing >>= half);
// Nothing
What's happening inside? Monad defines a bind (or >>=) function:
Let's make our Maybe into a monad by adding the bind functions.
let bind = (mv, f) => {
switch (mv) {
| Nothing => Nothing
| Just(v) => f(v)
};
};
let (>>=) = bind;
Here it is in action with a Just(3)!
And if you pass in a Nothing it's even simpler:
You can also chain these calls:
Maybe.(Just(20) >>= half >>= half >>= half);
Cool stuff! So now we have implemented Maybe to be a Functor, an Applicative, and a Monad.
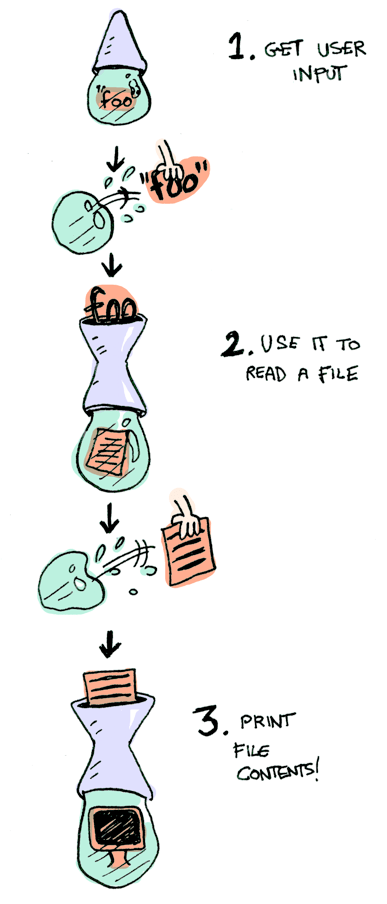
Now let's mosey on over to another example and create an IO monad:
The IO monad exists in Haskell, but we will declare our own in ReasonML.
Specifically three functions. getLine takes no arguments and gets user input:
readFile takes a string (a filename) and returns that file's contents:
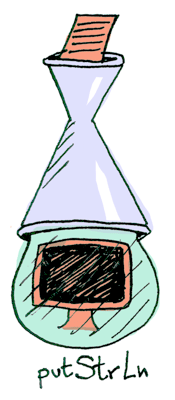
putStrLn takes a string and prints it:
Our IO module might look something like this (leaving out implementation details of the helper functions):
module IO = {
type t = Js.Promise.t(string);
type bind('a, 'b) = (t, string => t) => t;
let bind: bind('a, 'b) = (pa, f) => pa |> Js.Promise.then_(a => f(a));
let (>>=) = bind;
type getLine = unit => t;
let getLine = ...
type readFile = string => t;
let readFile = ...
type putStrLn = string => t;
let putStrLn = ...
};
If you're interested, the full source code is available.
All three functions take a regular value (or no value) and return a wrapped Promise value. We can chain all of these using >>=!
IO.(getLine() >>= readFile >>= putStrLn);
Aw yeah! Front row seats to the monad show!
Conclusion
- A functor is a data type that implements the
fmapfunction. - An applicative is a data type that implements the
applyfunction. - A monad is a data type that implements the
bindfunction.
The Maybe module in our examples implements all three, so it is a functor, an applicative, and a monad.
What is the difference between the three?
Functors: you apply a function to a wrapped value using fmap or <$>.
Applicatives: you apply a wrapped function to a wrapped value using apply or <*>.
Monads: you apply a function that returns a wrapped value, to a wrapped value using bind or >>=.
So, dear friend (I think we are friends by this point), I think we both agree that monads are easy and a SMART IDEA(tm). Now that you've wet your whistle on this guide, why not pull a Mel Gibson and grab the whole bottle. Check out LYAH's section on Monads. There's a lot of things I've glossed over because Miran does a great job going in-depth with this stuff.
If you feel there is something I could change to improve this translation to ReasonML please let me know.
Thanks again to Aditya Bhargava for writing the original version of this post ❤️




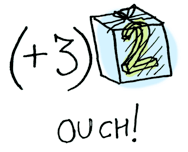



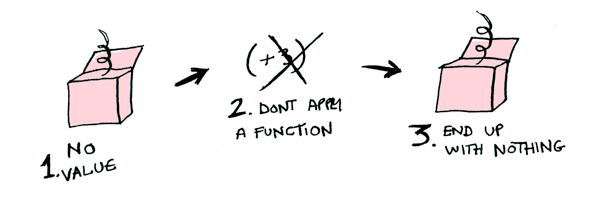
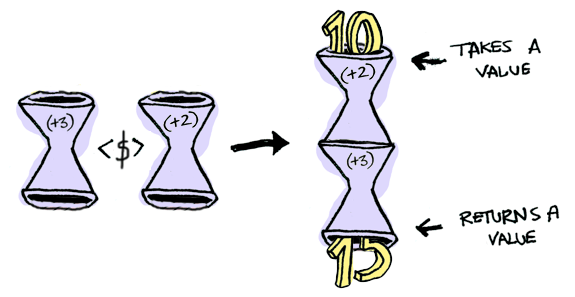



















Top comments (3)
Thank you for such a fun and understandable explanation!
Thank you for this.
One remark: I would add a note that the Maybe type is called Option in ReasonML, Just is equivalent to Some and Nothing to None.
Edit: And bind is (sometimes) called flatMap.
nice