Recapitulando...
Na semana passada, tivemos o primeiro contato com algoritmos de ordenação e busca binária(você pode conferir aqui).
Recursividade
A recursividade é uma ferramenta de programação que utiliza a reutilização do bloco de código para criar um processo de repetição de uma rotina de código. O conceito pode ser complexo, mas é apenas a criação de um laço a partir de um trecho de código e não de uma estrutura.
Caso você queira se aprofundar no assunto de recursão:
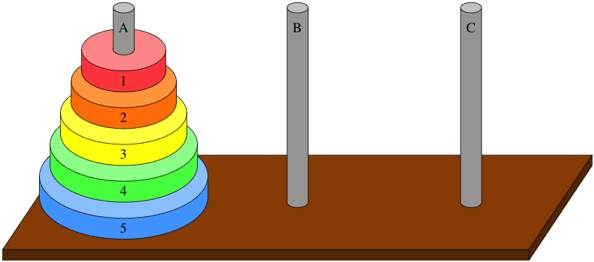
Um exemplo clássico de recursividade é a torre de hanoi. Sim, aquele brinquedinho de bebê. A torre de hanoi é o melhor exercício de recursividade que você pode treinar. Se você quer uma ajuda com a torre de hanoi:
Pilha de recursão
Ao trabalhar com recursividade, temos a necessidade de trabalhar com a pilha de recursão. Nós já estudamos pilhas como estrutura de dados no capítulo anterior. Hoje vemos uma estrutura semelhante, só que trabalhando com o empilhamento das chamadas de uma função recursiva. Para se aprimorar mais, temos:
Um exemplo de utilização ao máximo da pilha de recursividade, temos o caso do fibonacci. Ela se vale da pilha para calcular uma resposta. Vamos dar uma olhada mais afundo no algoritmo de fibonacci:
Algoritmo de divisão e conquista e Quicksort
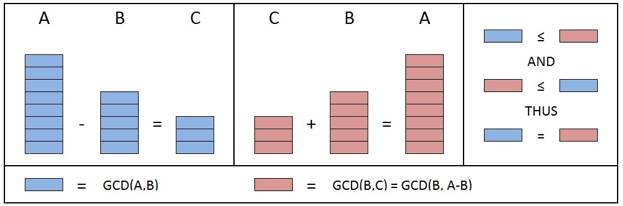
O algoritmo de divisão e conquista é um algoritmo que trata a divisão de um problema em vários probleminhas de mais fácil resolução. Baseado no algoritmo de euclides, que também é um dos algoritmos matemáticos interessantes para o estudo.
O algoritmo de divisão e conquista é a base de vários outros algoritmos, incluido o Quicksort, que foi o algoritmo estudado pelo livro. Se você quer saber mais sobre o quicksort, acesse:
Além do Quicksort, há um segundo algoritmo muito importante, o Mergesort. O mergesort é um dos algoritmos mais pedidos em provas técnicas, pois ele te promete um algoritmo de custo baixo O(nlogn), com um bonus de não exceder tanto a memória demandada. O quick é relativamente mais rápido, porém gasta muito com o recurso de memória, onde o merge entra para ajudar. Para saber mais sobre o mergesort, acesse:
Em uma classe diferente de algoritmos de ordenação, temos um algoritmo famoso pelo seu baixo custo, o counting sort. Seu custo é estimado em O(n + k) onde k seria uma constante calculada através do tamanho da lista. Ou seja, se a lista tem 10 elementos o custo do algoritmo seria O(n + 10). Um ótimo algoritmo, com um crescimento linear, não é? sim, mas como tudo que é bom tem seu preço, o algoritmo countingsort vai cobrar na memória utilizada. Para saber mais sobre este algoritmo, dá uma olhada neste material:
O coutingsort tem variações, que melhoram este problema de memória. O bucketsort e o radixsort. Eles irão trabalhar com estruturas de dados auxiliares que já vimos no capítulo anterior, linkedlist e arraylist, para fazer essa otimização. Para saber mais sobre, acessem:
-bucketsort e radixsort
Tabelas hash
Se você já programa a algum tempo, já deve ter topado com a estrutura de dados Map, ou dictionary, ou simplesmente tabela hash. Mas porque ela é tão importante? A tabela hash nos garante o acesso a um valor salvo e catalogado anteriormente ao preço de O(1). Ou seja, o acesso é instantâneo. Isso se dá pelo método em que traduzimos o valor da chave (key) em um endereço de memória e salvamos o seu conteúdo no valor resultante. Este método de calculo chama hashcode. Se você que saber mais alguns detalhes sobre a tabela e como fazer um hashcode, olha o link:
Conclusão
A maioria dos assuntos aqui são um incremento ao assunto principal abordado no livro atual do clube do livro. Caso você não esteja acompanhando o livro, mas se interesse sobre os assunto, até o momento temos estes artigos lançados:
Caso queira acompanhar nosso clube na leitura do livro, se sinta convidado a entrar para o discord:
Caso queira adquirir o livro, peça pelo nosso link. O valor adquirido pelo link de patrocinado vai ser revertido a livros para pessoas de baixa visão ou que tenham alguma deficiência para a utilização de meios ... não ortodoxos de leitura.





Top comments (6)
Acho algoritmos um dos assuntos essenciais para um bom dev, muito bom ter mais assunto até pq eu to devendo os estudos e com certeza esse artigo é bem útil pra mim ehehehe
Algoritmos definitivamente são um assunto que não domino, tem sido uma experiência incrível ler e aprender com sua didática incrível
Tem sido incrível partilhar esse pedacinho de conhecimento também 💙
Muito bom! Tem sido muito legal estudar com vocês, obrigado mais uma vez por puxar essa iniciativa, está me motivando muito a estudar, e está sendo beeeem divertido 😁
Aaah ❤️ fico feliz que você está gostando! Está sendo realmente muito legal ler em conjunto e trocar todo aquele conhecimento
Eu discordo da sua comparação entre o quicksort e o mergesort. Olhando o site Big-O Algorithm Complexity Cheat Sheet, na última coluna da tabela de comparação dos algoritmos de ordenação temos a complexidade de espaço desses algoritmos, onde a complexidade do quicksort é
O(log2 n)e do mergesort éO(n), logo o mergesort usa mais memória que o quicksort, pelo menos para listas maiores. Porém uma vantagem do mergesort é que o pior caso dele tem complexidade de tempo de execuçãoO(n log2 n), enquanto do quicksort éO(n²), logo o quicksort, em casos específicos, pode chegar a rodar tão lento quando a ordenação por seleção. Também deixo como curiosidade que o Python usa internamente o timsort, que é uma mistura entre o quicksort e o mergesort, consumindo um pouco mais de memória que o quicksort, porém sem a desvantagem do seu pior caso, e em casos específicos ele pode chegar a rodar emO(n), que seria o equivalente a só verificar que a lista já está ordenada e não fazer mais nenhuma operação além disso.