Se você já fez alguma matéria de algoritmos ou estrutura de dados, ou só brincou com ordenação, já deve ter ouvido falar de Bubble Sort: uma solução bastante ineficiente para o problema de ordenação.
Na verdade, existem várias outras soluções para este problema, mas resumidamente aqui está uma tabela comparando o tempo de complexidade de alguns algoritmos de ordenação:
| Algoritmo | Execução |
|---|---|
| Bubble Sort | O(n^2) |
| Insertion Sort | O(n^2) |
| Selection Sort | O(n^2) |
| Heap Sort | O(n log_2 n) |
| Merge Sort | O(n log_2 n) |
| QuickSort | O(log2 n) |
É bastante fácil de notar que de maneira geral os algoritmos de ordenação simples tem complexidade n^2, enquanto outros como Merge Sort n log_2 n, apesar da complexidade, cada um tem um desempenho melhor ou pior em cada caso. Mas...
Dá para ser tão pior que Bubble Sort?
A resposta curta: ✨ dá ✨
A resposta longa: existe um algoritmo chamado Stooge Sort. E ele funciona da seguinte maneira: sua lógica lembra o Bubble Sort, sempre faz a comparação de posições do arranjo em pares, e procurando o maior elemento, porém implementado de forma recursiva.
O pseudocódigo dessa criaturinha é o seguinte:
Se o valor do primeiro item for maior do que o último:
trocar o primeiro e o último valor;
Se o arranjo possuir 3 elementos ou mais:
recursivamente chamar stooge sort com os primeiros 2/3 do arranjo;
recursivamente chamar stooge sort com os últimos 2/3 do arranjo;
recursivamente chamar stooge sort com os primeiros 2/3 do arranjo;
retornar arranjo;
E sua implementação em C++ fica assim:
void stoogeSort(int arr[], int left, int right){
if (left >= right) return;
if (arr[left] > arr[right]) swap(arr[left], arr[right]);
if ((right - left + 1) > 2){
int t = floor((right - left + 1)/3);
stoogeSort(arr, left, right - t);
stoogeSort(arr, left + t, right);
stoogeSort(arr, left, right - t);
}
}
Sua complexidade é de O(n^2.7), e isso quer dizer que ele é pior que o Bubble Sort. Olhando para os números, não parece ter tanta diferença de O(n^2) e O(n^2.7), certo?
Bom, pode não parecer tão pior, mas para isso precisamos testar 😄.
Os testes
Os testes foram executados em uma máquina com as seguintes configurações:
LSB Version: n/a
Distributor ID: ManjaroLinux
Description: Manjaro Linux
Release: 21.2.6
Codename: Qonos
-----------
Arquitetura: x86_64
Modo(s) operacional da CPU: 32-bit, 64-bit
Tamanhos de endereço: 43 bits physical, 48 bits virtual
Ordem dos bytes: Little Endian
CPU(s): 6
Lista de CPU(s) on-line: 0-5
ID de fornecedor: AuthenticAMD
Nome do modelo: AMD Ryzen 5 3500X 6-Core Processor
Família da CPU: 23
Modelo: 113
Thread(s) per núcleo: 1
Núcleo(s) por soquete: 6
Soquete(s): 1
Step: 0
Aumento de frequência: habilitado
CPU(s) scaling MHz: 87%
CPU MHz máx.: 4520,8979
CPU MHz mín.: 2200,0000
BogoMIPS: 7902.79
----------
MemTotal: 16356904 kB (a.k.a 16GB de ram :))
O plano era executar todos os algoritmos para os seguintes cenários: listas de 10, 100, 1000, 10.000, 100.000 e 1.000.000 números não repetidos e não ordenados. Porém o Stooge Sort não colaborou, você pode ver os resultados no Github em números reais, neste arquivo e também neste mas o que vale a pena mencionar é que para ordenar o arranjo de 100.000 números o Stooge Sort levou 155662 segundos, convertendo isso dá mais ou menos 43 horas (vale a pena mencionar que o tempo medido é de processador, não de relógio), e devido a isto, os testes foram realizados apenas até o arranjo de 100.000 números. O interessante é que o Bubble Sort que é bem ruim, levou apenas 32 segundos para ordenar o mesmo arranjo. É uma diferença enorme né?
Tendo dito isso, mostrar o gráfico comparando os tempos de todos os algoritmos é até sem graça... pois ele ficou um pouco esticado:
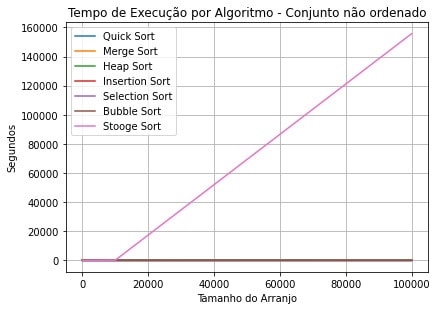
Basicamente o Stooge Sort é mais lento que todos os algoritmos na maioria dos cenários testados, e não é um pouco pior: na verdade é ridiculamente pior, apesar disso é um algoritmo interessante como objeto de estudo :), você pode ler mais sobre o Stooge Sort nas referências abaixo.
Referências
https://www.ijitee.org/wp-content/uploads/papers/v8i12/L31671081219.pdf







Top comments (2)
Existem algoritmos ainda piores que o Stooge Sort. Um exemplo é o Bogosort, que consiste em ficar embaralhando a lista aleatoriamente enquanto ela não estiver em ordem.
Sim, este é bem ruim mesmo :D