In this article, I embark on a nostalgic journey back to the 80s, using the Commodore 64 (C64) to solve mathematical challenges. Building on the success of my previous article, where I tackled proportion problems, I now dive into creating a calculator capable of computing approximate square roots and factoring them into factors using Assembly language.
Formulation of the Problem.
I was inspired to push the boundaries further after successfully solving proportion problems in my last article. I aimed to harness the power of the C64 to develop a calculator that efficiently calculates square roots, a frequently demanded operation in various mathematical domains.
Additionally, I sought to enable the factorization of square roots, a more accurate solution, which proves valuable in fields like trigonometry, signal processing, electrical circuit calculations, and optimization calculations. Function for calculation of square root numerical approximate value have every calculator.
To factorize the square root into factors, special tools are already needed. So the corresponding program for C64 is handy.
The Solution
Algorithm
The core algorithm I adopted is as follows:
Obtain the root of the number ‘x’.
Find an approximate answer using the built-in BASIC SQR function.
For factorization in the loop, do the following:
Traverse integers from 1 to ‘x’ and identify the maximum number whose square is a factor of ‘x’.
Determine the second multiplier as ‘x’ divided by the square of the maximum factor.
Prepare answer:
The first part of the answer is the square root of the square of the maximum factor.
The second part lies under the square root and is the second factor.
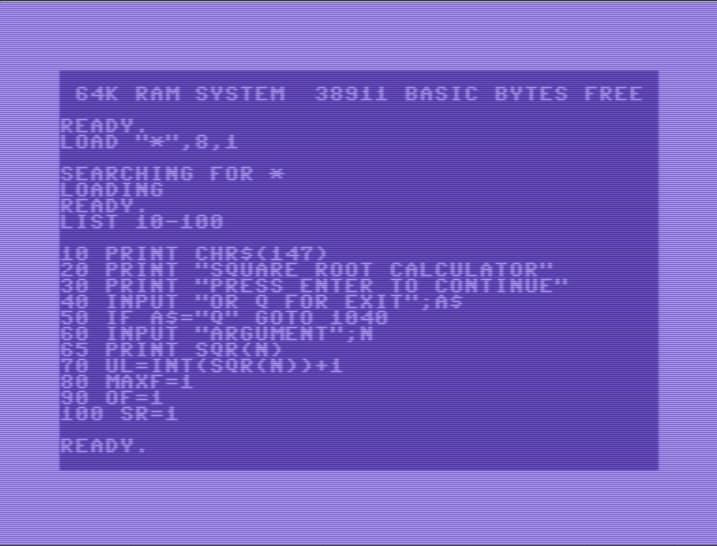
Implementation on BASIC
On BASIC, the program takes shape as follows:
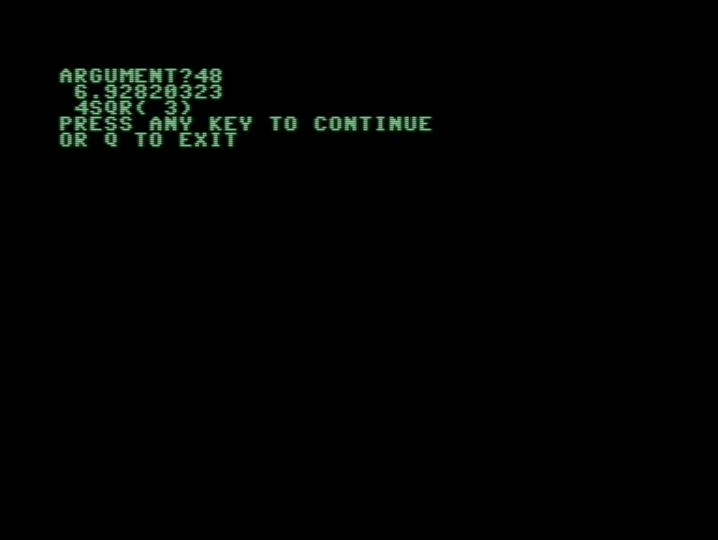
To simulate the modulo operation in BASIC, I used the following construction: A % B = A — INT(A / B) * B. Modulo is used to determine whether a number is a factor of the argument or not. The result of running the program looks like this:
The cycle is already noticeable in the delay between the approximate answer and the factorized one, even on big numbers.
Implementation On Assembly
Building on the procedures developed in my previous article, I focused on the primary algorithm implementation.
The implementation is as follows:
*= $1000
main:
jsr prepare_screen
jsr main_usage
wait_for_continue:
jsr getin
beq wait_for_continue
cmp #q_sym
beq go_to_exit
jmp get_args
go_to_exit:
jmp restore_and_exit
get_args:
jsr get_argument
jsr init_variables
//calculate and print sqr(argument)
lda #<argument
ldy #>argument
jsr fp_load_ram_to_fac
jsr fp_sqr
ldx #<ul
ldy #>ul
jsr fp_store_fac_to_ram
jsr fp_fac_print
//ul = int(sqr(argument)) + 1
lda #<ul
ldy #>ul
jsr fp_load_ram_to_fac
jsr fp_int
lda #<one
ldy #>one
jsr fp_add
ldx #<ul
ldy #>ul
jsr fp_store_fac_to_ram
The first block involves:
Preparing screen.
Retrieving the argument from the user.
Initializing variables with a value of 1.
Calculating the approximate square root value using the BASIC function.
Setting the upper limit for the factorization loop.
The subsequent block features the factorization loop:
loop: // for mf=1 to ul
//x = mf^2
lda #<mf
ldy #>mf
jsr fp_load_ram_to_fac
lda #<mf
ldy #>mf
jsr fp_mult
ldx #<x
ldy #>x
jsr fp_store_fac_to_ram
//y = int(argument) / int(x)
lda #<argument
ldy #>argument
jsr fp_load_ram_to_fac
jsr fp_int
ldx #<y
ldy #>y
jsr fp_store_fac_to_ram
lda #<x
ldy #>x
jsr fp_load_ram_to_fac
jsr fp_int
lda #<y
ldy #>y
jsr fp_div
ldx #<y
ldy #>y
jsr fp_store_fac_to_ram
//if argument - int(y) * x <> 0 goto next iteration
lda #<y
ldy #>y
jsr fp_load_ram_to_fac
jsr fp_int
lda #<x
ldy #>x
jsr fp_mult
lda #<argument
ldy #>argument
jsr fp_subst
lda #<zero
ldy #>zero
jsr fp_cmp
cmp #$0
bne not_factor
lda #<x
ldy #>x
jsr fp_load_ram_to_fac
ldx #<maxf
ldy #>maxf
jsr fp_store_fac_to_ram
not_factor:
lda #<mf
ldy #>mf
jsr fp_load_ram_to_fac
lda #<one
ldy #>one
jsr fp_add
ldx #<mf
ldy #>mf
jsr fp_store_fac_to_ram
lda #<ul
ldy #>ul
jsr fp_cmp
cmp #$1
bne go_to_loop
jmp end_loop
go_to_loop:
jmp loop
end_loop:
The Assembly code mirrors the functionality of the corresponding BASIC loop. Floating-point number comparisons are conducted using a BASIC function, and the results in register A are tested using a simple comparison operator.
Then I calculate and store both parts of the result.
//sr = int(sqr(maxf))
lda #<maxf
ldy #>maxf
jsr fp_load_ram_to_fac
jsr fp_sqr
jsr fp_int
ldx #<sr
ldy #>sr
jsr fp_store_fac_to_ram
//of = int(argument)/int(maxf)
lda #<argument
ldy #>argument
jsr fp_load_ram_to_fac
jsr fp_int
ldx #<of
ldy #>of
jsr fp_store_fac_to_ram
lda #<maxf
ldy #>maxf
jsr fp_load_ram_to_fac
jsr fp_int
lda #<of
ldy #>of
jsr fp_div
jsr fp_int
ldx #<of
ldy #>of
jsr fp_store_fac_to_ram
Results output:
//result output
lda #<sr
ldy #>sr
jsr fp_load_ram_to_fac
lda #<one
ldy #>one
jsr fp_cmp
cmp #$1
bne next_part
lda #<sr
ldy #>sr
jsr fp_load_ram_to_fac
jsr fp_to_str
jsr print_str
next_part:
lda #<of
ldy #>of
jsr fp_load_ram_to_fac
lda #<one
ldy #>one
jsr fp_cmp
cmp #$1
bne end_of_output
lda #<result_string_1
ldy #>result_string_1
jsr print_str
lda #<of
ldy #>of
jsr fp_load_ram_to_fac
jsr fp_to_str
jsr print_str
lda #right_p_sym
jsr print_char
end_of_output:
lda #new_line
jsr print_char
Here I’m ignoring the part of the result which equals one because it doesn’t matter when factoring.
Here is the output of the program:
Assembly program compiles to 2864 byte binary file. The delay is also visible in large numbers but much less than in the BASIC implementation.
Here is the complete source code of the program.
Conclusion.
While BASIC provides valuable tools for solving simple mathematical problems, the ability to call BASIC functions from Assembly code saves effort and allows for compact, fast programs.
My journey through the 80s, reviving mathematical programming on the C64, has been enjoyable and rewarding. To further improve my skills, I aim to delve into assembly 6510 (6502) and find relevant books to fill any knowledge gaps.
As I continue my exploration of mathematical programs for C64, I invite you to stay tuned for my future posts. The excitement of revisiting the 80s has given me ample reasons not to return to our time.
Until next time, warm regards and happy programming!












Top comments (0)