As a learning task, I start to search and try to improve functions speed to get Fibonacci numbers.
Fibonacci's numbers are a sequence of whole numbers arranged as:-
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
so the first thing dig into my mind is to try iteration methods:
package main
import "fmt"
func fibonacci(n int) int {
fn := make(map[int]int)
fn[0] = 0
fn[1] = 1
for i := 2; i <= n; i++ {
var f = 0
f = fn[i-1] + fn[i-2]
fn[i] = f
}
return fn[n]
}
This is an easy function to calculate fn "Fibonacci" number starting from 0,1 and then one over the other up to fn(i).
it uses an easy method :
Fn = Fn-1 + Fn-2
where,
n > 1
The downside of this function is that it can calculate up to the fn(92) which is 7540113804746346429, after that number the result will be above the limit of an int value.
So the solution is to use "math/big" package.
func fibonacci(n int) *big.Int {
fn := make(map[int]*big.Int)
fn[0] = big.NewInt(0)
fn[1] = big.NewInt(1)
for i := 2; i <= n; i++ {
var f = big.NewInt(0)
f = f.Add(fn[i-1], fn[i-2])
fn[i] = f
}
return fn[n]
}
with the above function you can get the fn(1000) which will be :
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
the downside of the above function is that it will be very slow if you increase the number, my pc froze when trying to calculate fn(1e6).
Fortunately, there is a better method known as fast doubling I will not go deep to describe this method, you can check this article for more details although it is written for c++
we can implement the fast doubling as follows:
func fibonaccibinary(n int) *big.Int {
if n == 0 {
return big.NewInt(0)
}
num := uint(n)
mask := bits.RotateLeft(1, bits.Len(num)-1)
a, b := big.NewInt(0), big.NewInt(1)
for mask > 0 {
c := Mul(a, Sub(Mul(b, big.NewInt(2)), a))
d := Add(Mul(a, a), Mul(b, b))
a = c
b = d
if num&mask > 0 {
a, b = b, Add(a, b)
}
mask /= 2
}
return a
}
if you want to further speed up the function we can change mask /=2 to mask >>= 1 and the method of calculating the mask (mask := bits.RotateLeft(1, bits.Len(num)-1)) is much faster than the one suggested in the mentioned article:
//slower than mask := bits.RotateLeft(1, bits.Len(num)-1)
func getmask(n int) int {
h := 0
for i := n; i > 0; i >>= 1 {
h++
}
mask := 1 << (h - 1)
return mask
}
I have to mention that using :
mask = bits.RotateLeft(mask, -1)
is faster than( mask >>= 1 ) but we should be careful that
//if mask = 1
bits.RotateLeft(mask, -1) != mask >>= 1
If we review the last function there are two calculations that take significant time:
c := Mul(a, Sub(Mul(b, big.NewInt(2)), a))
d := Add(Mul(a, a), Mul(b, b))
so it is better to use what Golang shine in (goroutine) to make these calculation happen concurrently.
Also, we are calculating fn(i+1) in the last loop iteration.
so to implement these enhancements we can go for:-
func fibonaccichanggoroutin(n uint) *big.Int {
if n == 0 {
return big.NewInt(0)
}
// num := uint(n)
chA := make(chan *big.Int)
chB := make(chan *big.Int)
a, b := big.NewInt(0), big.NewInt(1)
// There is only one `1` in the bits of `mask`. The `1`'s position is same as
// the highest bit of n(mask = 2^(h-1) at first), and it will be shifted right
// iteratively to do `AND` operation with `n` to check `n_j` is odd or even,
// where n_j is defined below.
mask := bits.RotateLeft(1, bits.Len(uint(n)-1))
for {
if mask == 1 {
// we are on last iteration wee need to just calculate a
if n&mask > 0 { // n_j is odd: k = (n_j-1)/2 => n_j = 2k + 1
a = Add(Mul(a, a), Mul(b, b))
} else { // n_j is even: k = n_j/2 => n_j = 2k
a = Mul(a, Sub(Mul(b, big.NewInt(2)), a))
}
return a
}
go CalA(a, b, chA)
go CalB(a, b, chB)
if n&mask > 0 { // n_j is odd: k = (n_j-1)/2 => n_j = 2k + 1
a = <-chB
b = Add(a, <-chA)
} else { // n_j is even: k = n_j/2 => n_j = 2k
a = <-chA
b = <-chB
}
mask = bits.RotateLeft(mask, -1)
}
}
func CalA(a, b *big.Int, ch chan *big.Int) {
ch <- Mul(a, Sub(Mul(b, big.NewInt(2)), a))
}
func CalB(a, b *big.Int, ch chan *big.Int) {
ch <- Add(Mul(a, a), Mul(b, b))
}
Finally you can check this repo for tests and benchmarks. the last function in this repo (func14) uses a table of precalculated Fibonacci numbers to speed up things...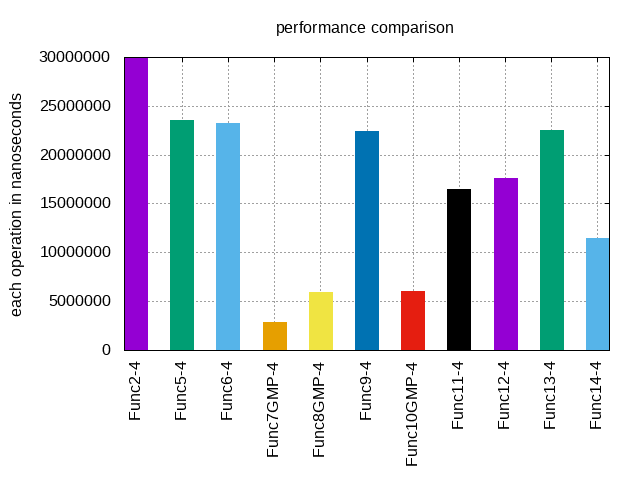






Top comments (0)