Parallelizing a serial pagerank implementation in C
Looking back through the years of studying Electrical and Computer Engineering and among many challenging projects, the last of the four total parallel and distributed systems project stands out.
The task was to parallelize a serial algorithm using one of the APIs we had used on previous projects during the semester, namely one of pthreads/cilk/openMP, cuda or openMPI.
Being a summer project, I chose to go with a single system CPU-parallelization API -and eventually openMP- so that I could work easily offline on my laptop without the need to access a cluster or a system with a specific GPU.
The project I went for was Pagerank calculation using the Gauss-Seidel method.
Pagerank
Pagerank was the original algorithm used by Google to rank websites so that it returns better search results. In brief, what it does, is to calculate a value for every page based on its in-going and out-going links. The basic idea being that the more a website is targeted by others the better the chance the content will be useful and what the user is looking for.
In other words, each link is like a special "vote" for the targeted website and the higher the rank of the website, the more its votes count for.

This may look like a cyclic dependency at first glance as each website's votes are weighted by its rating which is in turn affected by the incoming votes of other websites, that are also affected by their rating etc.
However, the math works out and the resulting rating of each website corresponds to the probability for an "internet traveler" to be at that particular website while moving around randomly through the available hyperlinks. A small chance of teleportation to any website is also applied, so that no website is left out and the traveler's behavior resembles more that of a real user browsing the web.
Creating a serial algorithm
In order to create an algorithm to solve our problem we first need a way to visualize and store the program's data. For this particular case, the intuitive way to do that is with a graph. Imagine each website being a different graph node and every link being a directed edge from the source to the target website.
Storing a graph in memory can be done in multiple ways and the best way will vary depending on the particular algorithm and system requirements. In any case, although the in memory representation of the graph may vary, they are all equivalent from a math perspective.
In our case, the traveler's trip can be simulated with a Markov Chain and reach a solution by solving a linear system derived from the Markov Chain's properties.
Gauss-Seidel Method
Having the linear system ready we can now solve it with a variety of methods, in this project the Gauss-Seidel iterative method was used.
In this method, the solution vector x for the system's table A is calculated many times until it converges to a value. Specifically, the k+1 step's solution vector is derived from the equality bellow:
The important thing about the expression above is that each next solution vector (step k+1) depends on its previous (step k) thus making the whole algorithm serial.
Identifying parallelization opportunities
After creating the serial algorithm it is important to first develop it and test it before trying to derive a parallel one from it. When this is done, we can start looking for ways to make the algorithm run on multiple cores.
But that may not be always possible with the selected serial algorithm.
This is also the case on our example here, the Gauss-Seidel method on a first glance looks completely serial. Before questioning our life choices that led as to this project, discard all our work and select a different project, it is a good idea to rethink about the problem and look for other parallelization opportunities that we may be missing.
Usually, the way this works is by trying to identify "independent patterns" on the task. Meaning, trying to split the problem in parts that can be solved or at least partially solved independently from the others. In our particular case, a such pattern is that the websites-links graph isn't a connected graph - meaning there exist groups of websites that only contain links within the group.
From the above observation we conclude that there shouldn't be a problem to calculate the rating of the websites within different groups independently and indeed this is the case.
Developing and testing the parallel algorithm
Great! Now we have a plan on our parallel approach. All that's left to do is develop it, test it and hopefully enjoy the speed up!
In this project, I used a simple graph coloring algorithm to identify independent groups of nodes that can be assigned to different threads and be picked up by different CPU cores. Finally, the CPU cores synced after every step, in order for the algorithm to behave exactly like the serial Gauss-Seidel one. In a non for-education project, that would not be needed and the resulting algorithm would be using a merge of the Gauss-Seidel and Jacobi methods.

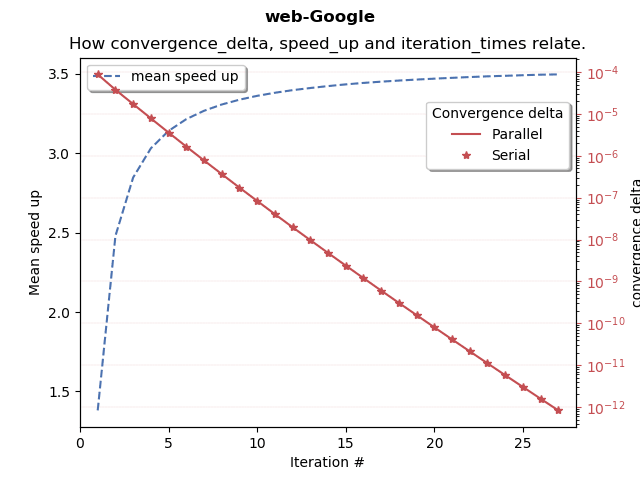
The results above correspond to a web graph of 875,713 websites and 4,563,235 links and the programs were compiled using GCC v.5.4.0 with the -O3 optimization flag enabled. The solution vector's convergence is also shown and is identical for both the parallel and serial versions of the program.
Link to Code
 nicktheway
/
Pagerank
nicktheway
/
Pagerank
A parallel C implementation using the Gauss Seidel method.
Pagerank Calculator
A C implementation of the pagerank algorithm with synchronous and asynchronous Gauss-Seidel iterations.
The algorithm needs the CRS representation of a graph in memory in order to compute its pagerank Methods for loading web-graphs into the memory that way are provided for a specific file structure Therefore, in order to load any web-graph, you might need to write a method that converts your web-graph file into a file of that structure For an example of such method check the already implemented one that converts files like the ones here.
For the parallel algorithm, a simple edge coloring algorithm has been written in a way that makes the algorithm equivalent to the serial one. Gauss-Seidel convergence speed depends on the order of the nodes too The best way to order the nodes is NP but there are heuristic greedy ways to do it. Non such way has been…
Notable headaches
Here is a non-exclusive list of issues I had to overcome while working on this project:
- How do I store and work with a table of up to about a million rows and columns?
Solution: Thankfully the table is sparse -> Used a compressed row storage (CRS) format.
- How do I support different formats of input data?
Solution: Created a special type of file optimized to be used by the program, then created a library for managing this new type of file. Can now work with any type of input by just providing a map function to the provided conversion program.
- Introducing the traveler's teleport ability makes it possible for the traveler to jump from any node to any other, doesn't that break the sparsity of the table?
Indeed it does, but as the teleport probability is equal for every node, there is a workaround equation that works with the original -no teleportation included- sparse table.
- Programming language headaches.
For the node-coloring I wished I could use C++ to make use of the standard library's vector structure, in the end I ended up creating a custom vector structure in C.
Tools that helped
- Git, even if used in a basic level, having version control usually makes life easier, this project was no exception.
- Doxygen, very easy way to generate code documentation. Here is this project's code doc.
- Github, version control and hosting the docs solution.
- GNU make, the standard compilation command wrapper.
- LaTeX, creating the project's report. All the latex files are included inside the git repo, here is the produced PDF. Although it is in Greek, the references titles are in English and can be found in the last page.







Top comments (0)