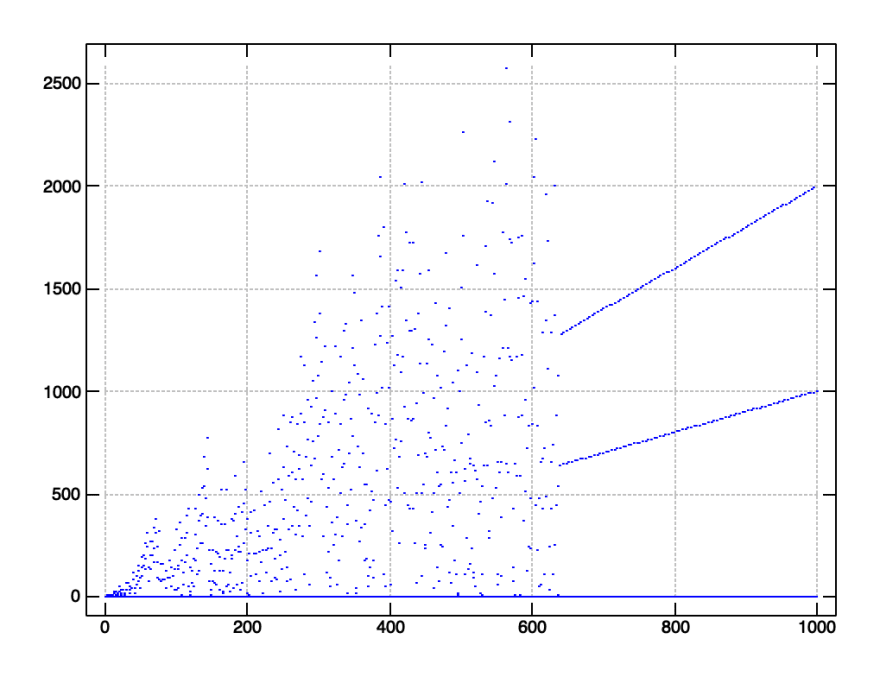
Numberphile recently posted a video about an interesting recursive function called “Fly Straight, Dammit!” which, when plotted, initially seems chaotic, but after six hundred thirty eight iterations, instantly stabilizes.
This sounds like a perfect opportunity to flex our J muscles and plot this function ourselves!
An Imperative Solution
The simplest approach to plotting our “Fly Straight, Dammit!” graph using the J programming language is to approach things imperatively:
a =: monad define
if. y < 2 do.
1
else.
py =. a y - 1
gcd =. y +. py
if. 1 = gcd do.
1 + y + py
else.
py % gcd
end.
end.
)
We’ve defined our a monadic verb to return 1 if we pass in a “base case” value of 0 or 1. Otherwise, we recursively execute a on y - 1 to get our py, or “previous y”. Next, we check if the gcd of y and py equals 1. If it does, we return 1 + y + py. Otherwise, we return py divided by gcd.
This kind of solution shouldn’t look too foreign to anyone.
Let’s plot values of a to verify our solution:
require 'plot'
'type dot' plot a"0 i. 1000
This works, but it’s very slow. We know that our recursive calls are doing a lot of duplicated work. If we could memoize the results of our calls to a, we could save quite a bit of time. Thankfully, memoizing a verb in J is as simple as adding M. to the verb’s declaration:
a =: monad define M.
...
)
Now our imperative solution is much faster.
Using Forks and Hooks
While our initial solution works and is fast, it’s not taking advantage of what makes J a unique and interesting language. Let’s try to change that.
The meat of our solution is computing values in two cases. In the case when y and py have a greatest common divisor equal to 1, we’re computing 1 plus y plus py. Our imperative, right to left implementation of this computation looks like this:
1 + y + py
We could also write this as a “monadic noun fork” that basically reads as “1 plus the result of x plus y:
a_a =: 1 + +
Similarly, when we encounter the case where the greatest common divisor between y and py is greater than 1, we want to compute py divided by that gcd. This can be written as a “dyadic fork”:
a_b =: [ % +.
We can read this fork as “x divided by the greatest common divisor of x and y.”
Now that we’ve written our two computations as tacit verbs, we can use the “agenda” verb (@.) to decide which one to use based on the current situation:
a_a =: 1 + +
a_b =: [ % +.
a =: monad define M.
if. y < 2 do.
1
else.
py =. a y - 1
has_gcd =. 1 = y +. py
py (a_b ` a_a @. has_gcd) y
end.
)
If has_gcd is 0, or “false”, we’ll return the result of py a_b y. Otherwise, if has_gcd is 1, we’ll return the result of py a_a y.
More Agenda
We can elaborate on the idea of using agenda to conditionally pick the verb we want to apply to help simplify out base case check.
<p>I find myself producing lots of ranging content from books and articles, like the one you're reading now, to open source software projects. If you like what I'm doing, <strong>nothing shows your support more than signing up for <a href="#newsletter">my mailing list</a></strong>.</p>
First, let’s define our base case and recursive case as verbs that we can combine into a gerund. Our base case is simple. We just want to return 1:
base_case =: 1:
Our recursive case is just the (memoized) else block from our previous example:
recursive_case =: monad define M.
py =. a y - 1
has_gcd =. 1 = y +. py
py (a_b ` a_a @. has_gcd) y
)
Our function, a wants to conditionally apply either base_case or recursive_case, depending on whether y is greater or less than one. We can write that using agenda like so:
a =: base_case ` recursive_case @. (1&<)
And because our base_case verb is so simple, we can just inline it to clean things up:
a_a =: 1 + +
a_b =: [ % +.
recursive_case =: monad define M.
py =. a y - 1
has_gcd =. 1 = y +. py
py (a_b ` a_a @. has_gcd) y
)
a =: 1: ` recursive_case @. (1&<)
Using agenda to build conditionals and pseudo-“case statements” can be a powerful tool for incorporating conditionals into J programs.
Going Further
It’s conceivable that you might want to implement a tacit version of our recursive_case. Unfortunately, my J-fu isn’t strong enough to tackle that and come up with a sane solution.
That said, Raul Miller came up with a one-line solution (on his phone) and posted it on Twitter. Raul’s J-fu is strong.





Top comments (0)