Finding the Beauty in Breaking it Down

Humans have a preoccupation with the big picture; the final product. When we imagine a problem - problem, in this case, being a loose term meaning a task to be completed - we often imagine it in the context of its answer. There’s nothing inherently wrong about this method of thinking, however, it can lend itself to feeling overwhelmed, inadequate, and stupefied.

I don’t think I’m alone in feeling like I may simply not be cut out for software engineering. The label itself - engineer - is never something I felt I could identify with. For most of my life, I’ve hardly even considered it. I’ve consistently rejected math and related disciplines in favor of more creative and open-ended fields, stemming from what I now recognize as insecurity and fear of problem-solving. Joining the world of programming has helped me break down the barrier to entry I’ve built when it comes to logical thinking, which has helped me immensely in building confidence and realizing my own potential. As a result, I recently decided to start learning more about calculus in my free time. I stumbled upon the YouTube channel 3Blue1Brown, which is dedicated to making digestible tutorials about mathematical concepts. The first video in the Essence of Calculus series details the breakdown of finding the area of a circle, which spawned a series of enlightenments regarding the beauty of breaking down problems.

Of course, I’ve always been familiar with the formula - πr² - but I’ve never really known what it means or why it works. Not only did I feel like I didn’t need to know what it means, but moreover I felt like I couldn’t know what it means, even if I had a need. Cue the bells of insecurity. But, Grant Anderson, the voice behind 3Blue1Brown, was adamant that after the tutorial we could feel as though we could discover the formula on our own accord given the perseverance. Much to my surprise, he was right.

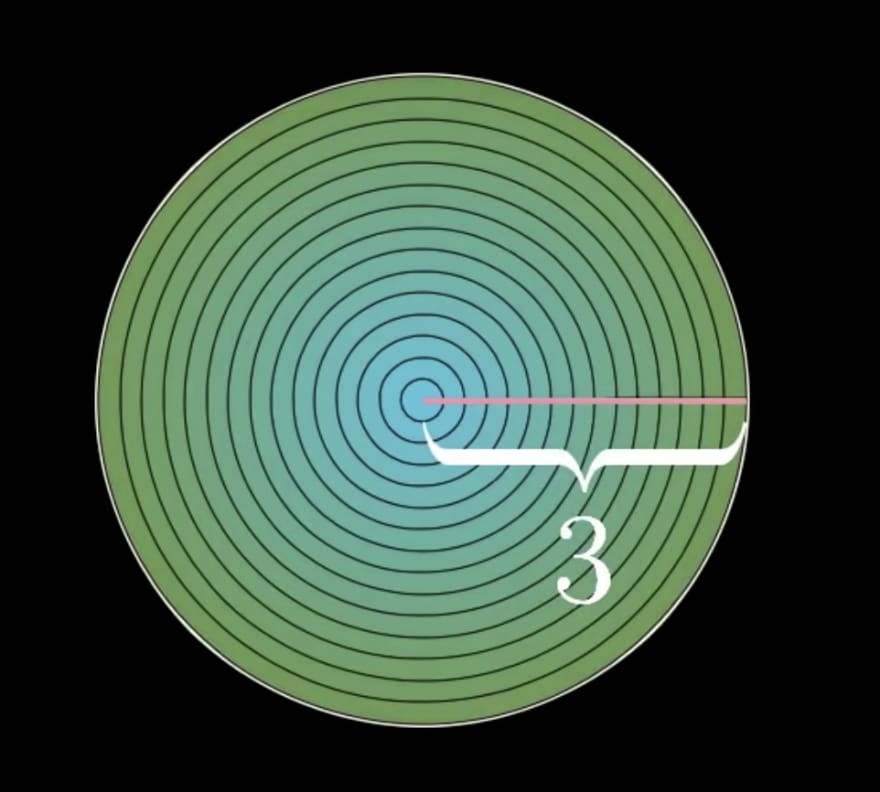
It starts with how we imagine a circle. If we think about it as many slivers of small rectangles, as visualized below, the problem already starts to unravel:

Rectangles are a familiar face. Finding the area of those is fairly simple - just length times width. For each rectangle, we can think of the length as being equal to the circumference of the given portion of the circle it represents (2πr, if you recall), and the height as being the difference in the radius - which changes based on how small our slivers are.

At this point, it is important to note that these are mere approximations. But, beginning with estimations is key to making problems more manageable; fine-tuning comes later. Anyway, moving forward, we have a circle broken down into rings, and further broken down into rectangles, whose length differed based on which part of the circle it represents; in other words, a range. What can we do with ranges to visually represent them? Well, we could graph them! Then, we end up with something like this:

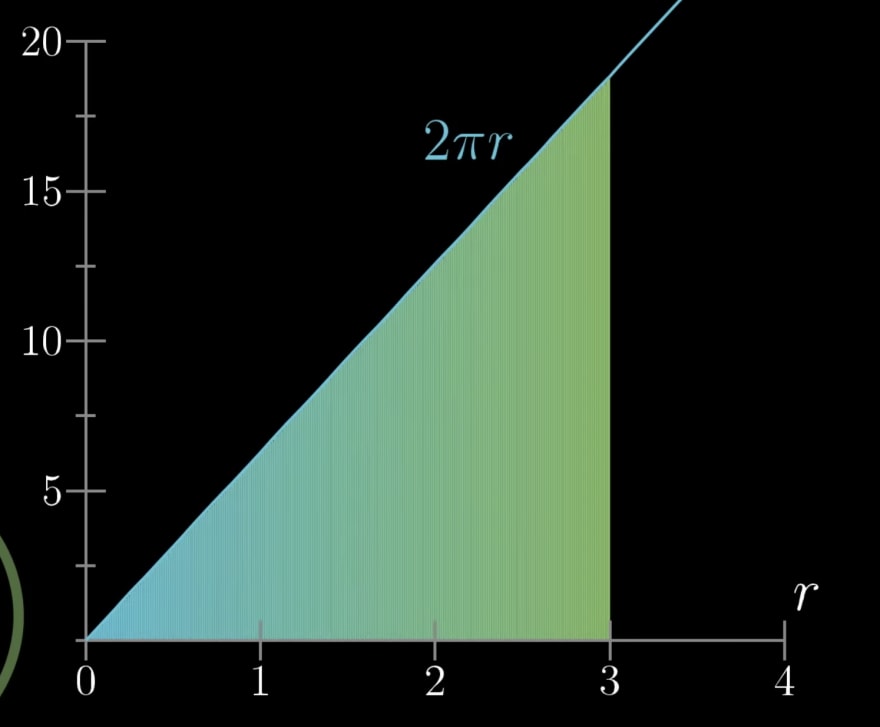
And here’s where the fine-tuning starts to come into play. The smaller we choose to make the slivers of rectangles, the more accurate this representation becomes. And, as we make them finer and finer, the graph starts to smooth out:

So comes another familiar face: a triangle. More specifically, a triangle with a base of the radius of the circle (3), and a height of 2π times said radius (2πr). Now, we already know how to find the area of a triangle - half the base times the height. After plugging in the appropriate values…

Look at that. We’ve come full circle (pun intended). As Grant states, “It doesn’t matter who you are, or what you think of math - that right there is a beautiful argument.”

And its beauty is the gift that keeps on giving. My primary takeaway from this lesson is not that I learned more about circles, or geometry, or even necessarily that I understood all of it. It is that succinctly put, a large problem is only the sum of many small problems.

The same thought process can be applied to programming. Much of programming is dealing with problems - building a functional program, creating associations, fixing a bug, traversing and transforming data, et cetera. As the abstraction grows, problems become increasingly daunting at every level. But, you hold the power to bring the problem down to eye-level. That may mean a class, a method, a conditional, or at its base level, a single line of code. Though we may be interacting with a problem at a high level, it is vital to remember that it is the aggregate of individual lines being executed - slivers of a larger whole. Break it down, understand it, and its veil will be lifted. Beauty, exposed.