Last 3 days have been invested in figuring out how to solve this particular problem posted on GeeksforGeeks , I will pen down my research and conclusion so that you don't have to invest 3 days like me .
Flow Of Explanation
Understanding the Question
Landing at the code
Final Code that got accepted
Understanding the Question
Minimise the Height II -
Given an array arr[] denoting heights of N towers and a positive integer K, you have to modify the height of each tower either by increasing or decreasing them by K only once. After modifying, height should be a non-negative integer.
Find out what could be the possible minimum difference of the height of shortest and longest towers after you have modified each tower.
There are few points you need to stress on while reading the question that i have underlined. Now what exactly does it mean ?
You have been given an array actually with few elements in it, You have been asked to create another array after modification.
The modifications can be made using " K " which is a positive integer , and make sure that the range of modified array is smaller than that of original one.
I will describe further and things will get clearer with time.
Remember : According to this question , each element of an array represents a building where the value describes the height of that building.
Let's first go with a small array and try to understand.
arr = [1,3,6] //serial id:1 (Original Array)
k = 3
range = 6(highest) - 1(lowest) = 5
The range is 5, which is the maximum range . Our goal is to minimise the range
Now we have to play with this array to understand it better . Now remember for each element we can either add K(+3) to them or subtract (-3) from them .
For Eg: arr[2] = 6 ; for this either the element at 2nd index can become 9(6 + 3) or 3(6 - 3).
Let's take a modifying array which will be serial id: 2
where a[0] + 3 =4 ; a[1] - 3=0 ; a[2] + 3=9
arr = [4 , 0 , 9] //serial id:2 (Modified array)
range = 9(highest) - 0(lowest) = 9
The range is 9 , which is more than the range of previous original array.
Our goal was to minimise it . Obviously 9 > 5 (Not our required answer)
So , what will be the correct modification . Let's add K(+3) with arr[0] ; add K(+3) with arr[1] ; subtract K(-3) from arr[2]
arr = [4 , 6 , 3] //serial id:3 (Modified array)
range = 6(highest) - 3(lowest) = 3
The range is 3 , which is less than the range of the original array(Serial id: 1)
Our goal was to minimise it . We have done it. 3 < 5 .
Pat on your back , phew. I know it still looks confusing . Just bear with me.
Logic that we will Implement
Let's take a bigger array to understand the problem . I hope you have understood the question and our goal by now .
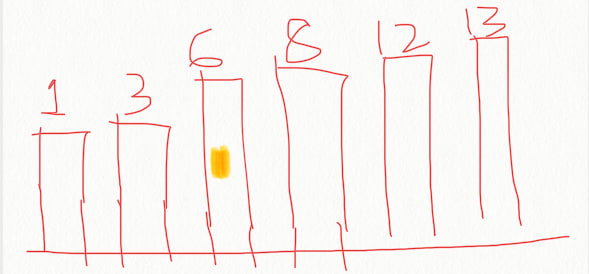
Example Array : arr[ ] = [1 , 3 , 6 , 8 , 12 , 13]
Here , also notice the array/ building elements heights are in sorted manner.
Incase the array input is not sorted , first step is to sort the array.
However it's sorted here .
Logic :
In the First image , you saw a yellow dot on building with 6 height. right? Now why was that for?
To understand the logic , we have to assume a maximum in the array . Let's assume the element at index 2 of array is the maximum . We know to find a range : We need one maximum value. & one minimum value
Max Value(assumed) : Element at index arr[2] i.e 6. But wait !! How can an element in the middle be maximum in a sorted array . Here is the catch . The element in the middle can be the highest when we use [K] , If we add +K , then there is a possibility that it becomes maximum .
Eg :
We have added +K to arr2 so it becomes {6 + 3}=9
We have added +K to minimum most value i.e arr[0] , so it becomes {1 + 3}=4
We have subtracted -K from the arr[3] value , as it's the next maximum element after our assumed maximum , so it becomes {8 - 3} = 5
Find the minimum value :
Now to find minimum value we have two options : Either the minimum most value will still hold the minimum most position in modified array orelse the element next to arr[2] .
We have to bring some element in the modified array close enough to the chosen maximum to minimise the difference.
Considering arr[2] is the maximum then either incrementing the first element in the array
that is arr[0] + K will become close to chosen maximum orelse decrementing the element next to
assumed maximum in array by K
First option is where we find a minimum value from the left of arr[2]
Now why we have taken the 0th element of array as option 1?
First of all after modification no element can be negative. so we can't subtract K from a[0].
Second , can we find any other element for minimum most height for the arr[2] element ? NO!!!Why ?
Because , it's sorted . See the only way to decrease the gap between heights of building , we have to increase the height of the building with low heights
Now , let's say you increase the height of arr[0] by K=3 and make it 4 , Also you add K=3 to arr[1] and make it {3+3} =6.
This example tells us , no matter what arr[0] will always be the smallest
Comparing the elements after modification . Now the modified arr[0] = 4 & arr[2] = 9 .
Range ? Range = 9 - 4 = 5
Second Option where we check if we decrease the height of building next to arr[2]{assumed maximum} then will it result in the minimum most element in the modified array .
If we want arr[2]=9(after modification) to be the maximum then we will have to ensure that everything after must subtract(-K) from it's value , orelse it can't stay maximum if anything after it adds (+K) to it.
Eg: If you add (+K) to building with height 8 then it will become 11 , similarly if you add (+K) to building with height 12 it will become 15 , which is obviously greater than our assumed tallest building which is modified arr[2] = 9.
To Decide The Minimum :
To decide option 1 is the minimum for our assumed tallest building arr[2] = 9 or option 2. we have to use the min(input 1 , input 2) function.
min(arr[0] + k , arr[3] - k);
This is written in context of where we assumed the tallest building after modification.
Ensure that arr[2] = 9 is the Tallest ! How ?
We will now play with the last element of sorted array , where the last element is the tallest building obviously. Like , arr[5]=13.
But why ???
We have assumed arr[2] to be our maximum right???
For {arr[2] + K} to be maximum we will run it through a comparison where we compare it with { arr[5] - k }. Because , arr[5] is the maximum element . If even after adding K from the assumed tallest {arr[2] + K} the assumed tallest is less than {arr[5] - K}.Then in that case arr[2] + K can never be the tallest building after modification. To be maximum it must suffice the condition :
(arr[2] + K > arr[5] - K)
We can ensure the maximum among two using max(input , input) function
max(arr[2] + k , arr[5] - k);
UNDERSTANDING THE CODE
1) SORT THE ARRAY
We have to sort the given array to us , in this example our given input was arr[ ] = [1 , 3 , 6 , 8 , 12 , 13], in this example it's sorted but not all inputs will be sorted. First sort the array .
sort(arr , arr + n); //sort(start address, ending address);
2)INITIALISE VARIABLES TO STORE MINIMUM & MAXIMUM VALUES
We declare two variables
int max_elem , min_elem ;
max_elem will store the output of max function & min_elem will store the output of min function.
3) INITIALISE AND DEFINE VARIABLE ans
We initialise variable ans and define it , store the difference between maximum element after sorting & minimum element.
int ans = arr[n-1] - arr[0] ; //13 -1 = 12 = ans(for this example)
You will know the need of this in the article further.
4) FOR LOOP
This is the most important to understand , we will run a for loop to iterate over each element of sorted array . In each iteration we will assume the (i)th element is the current maximum.
for(int i =0 ; i <= n-1); i++) {
min_value = min(arr[0] + k , arr[i+1] - k);
max_value = max(arr[i] + k , arr[n -1] - k);
}
In any case , we can't take the min_value as negative , what if subtracting K from any element will result in a negative number, This is against the question . Hence we add an if statement.
for(int i =0 ; i <= n-1); i++) {
min_value = min(arr[0] + k , arr[i+1] - k);
max_value = max(arr[i] + k , arr[n -1] - k);
if(min_value) < 0 continue;
}
We then take out the difference between max_value & min_value and compare it with our pre defined range stored in ans variable, which ever is the minimum gets stored in the ans variable.
for(int i =0 ; i <= n-1); i++) {
min_value = min(arr[0] + k , arr[i+1] - k);
max_value = max(arr[i] + k , arr[n -1] - k);
if(min_value) < 0 continue;
ans = min(ans , max_value - min_value);
}
Then return the ans.
A DRY-RUN WILL HELP YOU UNDERSTAND MUCH BETTER.
CODE








Top comments (0)