When you're coding you're going to use a lot of data. And when you're dealing with complex problems that use a lot of it, that data needs to be structured- you don't want it floating around all willy-nilly in the ether.

These data structures can be all kind of things, linked lists, arrays, hash tables. But today I'm going to be talking about trees: Binary Search Trees in particular, as one might of guessed from my uninspired title.

So, what the heck is a tree?

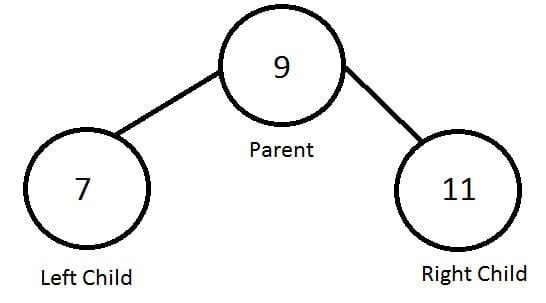
In computer science, a tree doesn't refer to those green leafy things you see scattered about the landscape, but rather a branching collection of nodes representing whatever values you're working with. These start with a singular root node (also called a parent) that is then connected to branches (or children) flowing downward.

Kinda like this, but with a lot more 1's and 0's

Where a Binary Search Tree, or BST's (much like military, coders love acronyms) differ is the amount of child nodes and how those nodes are structured. Each node in a BST can only have up to two nodes- that's where the binary part comes in- and are structured in such a way where the lower value is always to the left, higher to the right.

And this is how the above example might appear as a JavaScript object:

let parentNode = { 
value: 9,
leftChild: {value: 7},
rightChild: {value: 11}
}

Why the heck are they useful?

"So what's the big deal?", you might ask, "what makes BST's so special instead of an array or something similar?". Speed. Look-up speed in particular. Imagine if our tree wasn't just that one binary node, but a series of binary nodes, linked to more binary nodes, all structured in such a way that the lower value is always to the left, higher always to the right.

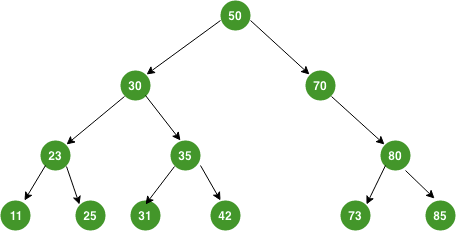Like this one right here

If this was structured in an array instead, we might have to iterate over every index to find the value of, say, 42. This would give us a linear big O time complexity or O(n). But using a BST we can check the if the value of each child node is higher or lower than 42, and each time eliminate an entire branch of the tree from our potential search. This gives us a logarithmic big O time complexity or O(log n).

Where the heck are they used?

"Well, that's cool and all", I can hear you saying, "but what good has a BST ever done for me?" Here's a few examples of some real world implementations of binary search trees:

*Radix Tree - Used in almost every high-bandwidth router for storing router tables

*Huffman coding - compression algorithm used in .jpeg and .mp3 file-formats

And my personal favorite:

*Binary Space Partition - Used in 3D video games to determine which objects to render. The first ever use of Binary Space Partition being 1993's Doom.

This means by the virtue of association, BSTs are "the number one cause of decreased productivity in businesses around the world"

So the next time you crawl away from the cold blue glare of you computer screen and get a brief glimpse of those green leafy things outside, imagine them being upside down and full of data you can look up quickly. And then crawl back inside and implement a BST to handle whatever massive set of data you're working with.