Better recursions with Tail Call Optimization

On a beautiful day in the Shire, Bilbo Baggins is learning programming and was practicing recursions.

He wrote this code

const fact = (num) =>{
  if(num === 1) return 1; // non-recursive base case
  return n * fact(n-1); // recursive part
}

So he ran it, it worked fine with 3 and 4.
But this curious headed little hobbit wants to check how long can it go.
He gave input of 100000 and

RangeException:
Maximum stack size exceeded

He ran to seek help from Gandalf, then the wise wizard explained to him how stacks work.

Whenever you call a function then it pushes a new frame on to the stack and once the operation of that frame is done then it is removed from the stack

So the above code for input "4" would translate into this

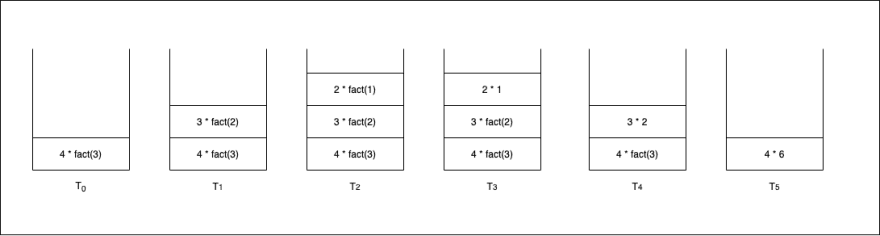
Since the ram has a limited size and it allocates a little part of it whenever a program runs. Keeping this restriction in mind, when you run the same code with input "100000" the stack length increases and eventually reaches a point where it cannot add any new frames into it.

And now Bilbo asks Master can we not optimize it?

The Gray one smokes the pipe and says Of course my old friend!

Tail Call Optimization
If the last thing a routine does before it returns is call another routine, rather than doing a jump-and-add-stack-frame immediately followed by a pop-stack-frame-and-return-to-caller.
Tail call optimization reduces the space complexity of recursion from O(n) to O(1). Our function would require constant memory for execution. It does so by eliminating the need for having a separate stack frame for every call.

So Gandalf rewrote the code

 const fact = (num,acc = 1) => {
     if(num === 1) return acc;
     return fact(n-1,acc * n);
 }

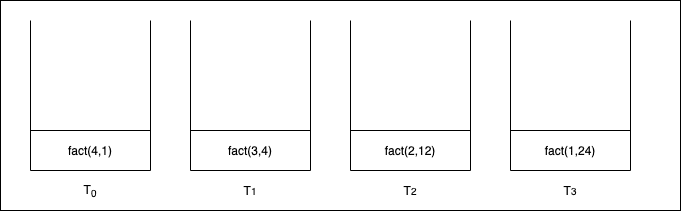
Now the stack view looks something like

Here whenever you call the fact function instead of adding a new frame on to stack the frame is removed from the stack since it is the last thing to be done by it.