Hi everybody, my name is Michael Roks, I'm a backend software engineer at Yandex with 5+ YOE, and an hobbyist competitive programmer!
Today we are going to talk about different ways to evaluate the Complexity of your algorithms, specifically - the Big-O Assymptotic Complexity VS. the Amortized complexity. Understanding this helps you get a better grasp on how the common data structures work inside, and it would be a plus for you to mention this in an interview :)
Speaking in simple terms, the Big-O analysis is the "Worst possible" complexity of the algorithm - Time and/or Space complexity. And the Amortized analysis is the "Average amount of work for 1 run, if we run K times".
For example, adding an element to a Dynamic Array is O(n) Time Complexity (I used the Big-O symbol O to denote the Big-O - Worst-case-scenario Asymptotic analysis notation), and Amortized(1) (There is no dedicated symbol for the amortized analysis, so I'm just putting the word Amortized in front of the complexity itself).
Why are the complexities like this?
It's because of how the Dynamic Array handles adding and removing elements. Quick reminder - the dynamic array, in its most simple form, has the following methods:
- Add to the end
- Remove from end
- Get by any index
As well as the dynamic array has the underlying "regular" array & a lastIndex pointer to the place in that "regular" array, denoting the location of the last item.
When you are adding to the end of the array, there are 2 ways it can go:
- You have spare space at the end of your "regular" array, you just write the provided element by
lastIndex, and do++lastIndex. - You ran out of the spare space in the "regular" array, and now have to
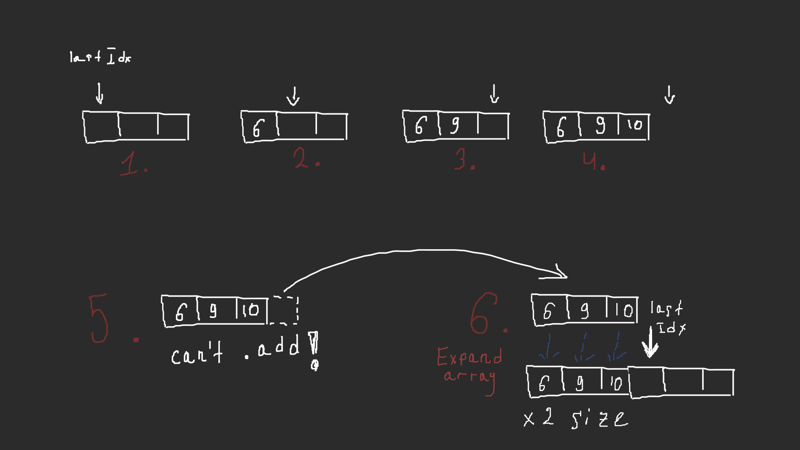
expand, and then append the provided element to the expanded array A visual example!
In steps 2,3 & 4 we successfully added elements by lastIndex and moved it 1 to the right. But then we ran out of space & had to Expand the underlying regular array (create a new one greater in size & copy all the existing elements into it).
As you can tell, the Expand operation is O(N) time complexity. As the Expand is eventually triggered by a single add operation, the add operation is also O(N), as O is the Worst-case-scenario notation. So adding to the dynamic array is O(N) operation.
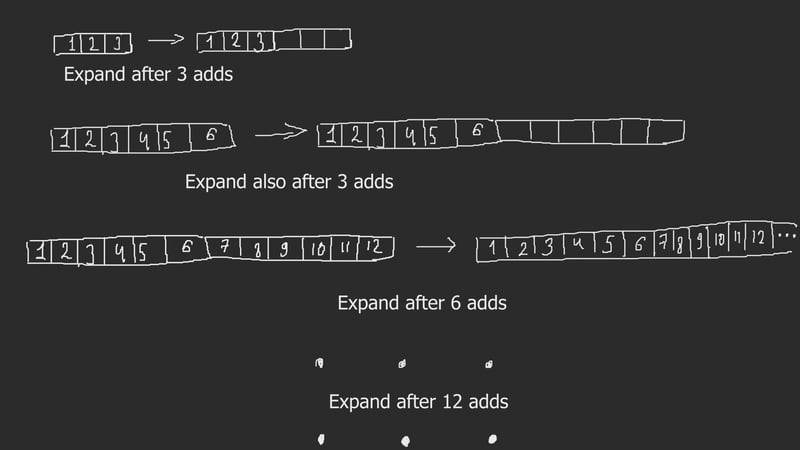
But next, let's look at how many expansions we have to do over K runs of add. In our example we started at size 3, and expand each time we fill up the dynamic array. Another visual example!
- Fill the initial array of size 3 (3 add operations), then expand (3 copy operations)
- Finish filling the array of size 6 (another 3 add operations), then expand (6 copy operations)
- Finish filling the array of size 12 (another 6 add operations), then expand (12 copy operations)
- Finish filling the array of size 24 (another 12 add operations), then expand (24 copy operations)
- Finish filling the array of size 48 (another 24 add operations), then expand (48 copy operations)
- And so on…
As you can see, continuing this series into the infinity, the total number of copy operations done because of K .add operations is ~2*K, so on average, adding an item to the end of a dynamic array requires 3 operations - 1 for adding & 2 for future expanding (as for K .add operations we require 3*K total amount of work)
And this is exactly what Amortized analysis is - the average amount of operations for 1 run over K runs. And this is the proof, that adding to the end of a dynamic array is Amortized(1) Time Complexity. Thank you for you time & attention! Plz like & share if you thought this is a good read :D







Top comments (0)