Zach, next time you come back to this, let's try to answer the question at the bottom
| Algorithm | ArrayList | LinkedList |
|---|---|---|
| seek front | O(1) | O(1) |
| seek back | O(1) | O(N) |
| insert at front | O(N) | O(1) |
| insert at back | O(1) | O(1) |
| insert after an item | O(N) | O(1) |
Why?
Arrays have O(1) random access, but are really expensive to add stuff onto or remove stuff from.
Linked lists are really cheap to add or remove items anywhere and to iterate, but random access is O(n).
This makes sense. Linked lists can only be searched sequentially. You have to search node-to-node, front-to-back -- O(n).
The 'problem' with arrays is that they have a fixed size. So when you manipulate the array from somewhere other than the very first/last item, it has to do a whole lost of work shifting elements around:
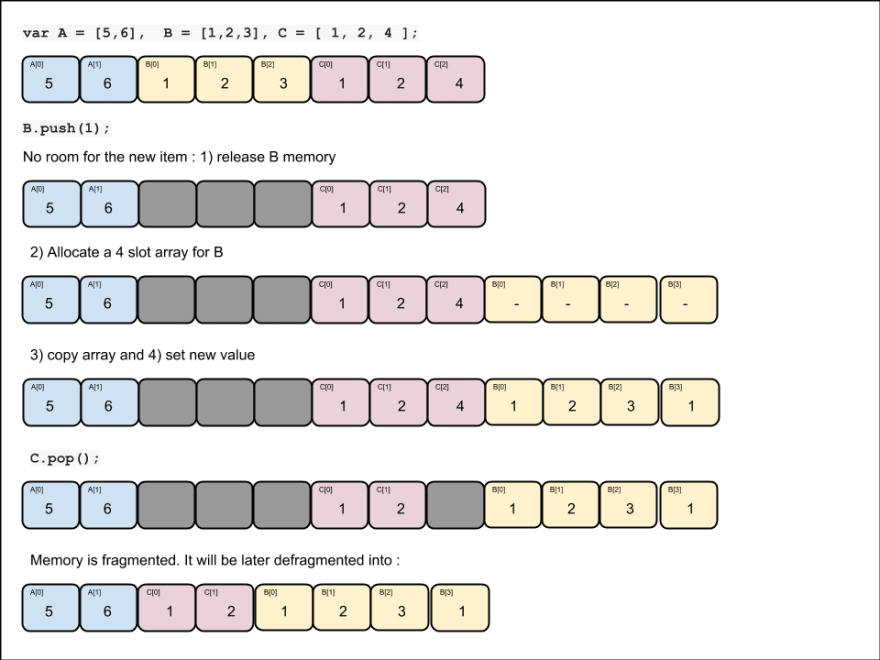
One important thing to notice, that is hidden by the simplicity of push(), pop(), among others, is that any time you change the size of an array it might lead to memory allocation and/or memory fragmentation and/or memory copy.
Exemple :
// let us allocate 3 arrays :
var A = [5,6], B = [1,2,3], C = [ 1, 2, 4 ];
// let's push a value on B :
B.push (1);
// let's pop a value on C :
C.pop();
those 3 lines of code will be handled like this :
This explains insert after an item: O(N). Shifting all those items around is a complex operation.
A question I have:
In order to insert in the middle of a linked list, don't you have to traverse the array to find the position? If so, isn't that an O(n) operation? So why wouldn't this cause insert to inherit the O(n) search cost that occurs before the actual insert?






Top comments (0)