Introduction
In this article I want us to look at my implementation of a Heap data structure in Go. I assume that you are already familiar with the theory behind what a Heap is and its properties but if you're not then I will try to briefly explain this to you below and also tell you about some resources where you can learn more.
What is a Heap
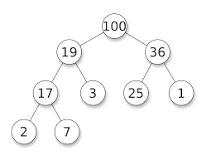
If I had to explain it in my own words, I would say that a Heap is a data structure which can be visualised as a nearly-complete binary tree (read my post on Trees) and stores its data in an underlying array. By looking at one, you would probably assume that it is based on a linked list, but in fact it is not. Using a Heap we can sort items at a O(n*logn) time complexity and also create priority queues.
We say that a Heap is a nearly-complete binary tree because the lowest level might not be complete, like in the example above.
Also, there are two types of heaps: Max Heap (see above) and Min Heap. The difference between them is that in a Max Heap, we have the largest element at the top, followed by smaller children. And in a Min Heap we have the smallest element at the top, with larger ones following.
For more information on heaps I recommend the following resources:
Abdul Bari's video explanation
MIT lecture on Heaps
Implementation
I have implemented both a Max Heap and a Min Heap in Go, but for the sake of brevity and because the implementations are very similar, I will only go through the Max Heap in this article. You can find both implementations, plus some other data structures in the repository below.
 dorin131
/
go-data-structures
dorin131
/
go-data-structures
A collection of data structures implemented in Go
go-data-structures
An implementation in Go of the following data structures:
- Linked List
- Stack
- Queue
- Binary Search Tree
- Graph
- Hash Table
- Min Heap
- Max heap
As I mentioned earlier, the Min and Max Heaps are quite similar, so I created a heap package that I shared between both of them using embedding.
Let's start with the heap package. In it I have created a Heap struct with an Items field of type slice of integers, which will hold all the values in our heap.
Also it has the Size field that holds the size of the heap. We need this because we might have elements in the Items slice which are not part of the heap. This is going to be used for sorting.
All the other methods in here are just helper functions that let us easily access elements in our Heap.
/*
Package heap provides helper methods for a Min Heap or a Max Heap
Not to be used on its own.
*/
package heap
// Heap : contains a slice which holds the underlying heap data
type Heap struct { // the total number of elements, which doesn't go down on extract
Items []int
}
// GetLeftIndex : get left index of a Heap node
func (h *Heap) GetLeftIndex(parentIndex int) int {
return 2*parentIndex + 1
}
// GetRightIndex : get right index of a Heap node
func (h *Heap) GetRightIndex(parentIndex int) int {
return 2*parentIndex + 2
}
// GetParentIndex : get parent index of a Heap node
func (h *Heap) GetParentIndex(childIndex int) int {
return (childIndex - 1) / 2
}
// HasLeft : check if node at index has left node
func (h *Heap) HasLeft(index int) bool {
return h.GetLeftIndex(index) < len(h.Items)
}
// HasRight : check if node at index has right node
func (h *Heap) HasRight(index int) bool {
return h.GetRightIndex(index) < len(h.Items)
}
// HasParent : check if node at index has parent node
func (h *Heap) HasParent(index int) bool {
return h.GetParentIndex(index) >= 0
}
// Left : get left node value, given an index
func (h *Heap) Left(index int) int {
return h.Items[h.GetLeftIndex(index)]
}
// Right : get right node value, given an index
func (h *Heap) Right(index int) int {
return h.Items[h.GetRightIndex(index)]
}
// Parent : get parent node value, given an index
func (h *Heap) Parent(index int) int {
return h.Items[h.GetParentIndex(index)]
}
// Swap : swap values of two nodes at specified indeces
func (h *Heap) Swap(indexOne, indexTwo int) {
h.Items[indexOne], h.Items[indexTwo] = h.Items[indexTwo], h.Items[indexOne]
}
Next we have the actual Max Heap package which is going to use the structure we created earlier.
It has two exported methods: Insert and ExtractMax, which let us add and retrieve values off the Heap.
But the most interesting methods are probably maxHeapifyUp and maxHeapifyDown. The first one starts at an index and pushes the value up the heap until it reaches a position where it is smaller than the parent and the children are are smaller than it is. And the second will also start at an index and push the value down until it gets into a position that satisfies the Max Heap data structure.
Lastly we have the buildMaxHeap method that takes any slice of integers and creates a Max Heap out of them. It is called every time we initialise a new heap with a pre-populated slice.
/*
Package maxheap provides a Max Heap data structure
*/
package maxheap
import (
"log"
"github.com/dorin131/go-data-structures/heap"
)
// MaxHeap : represents a Max heap data structure
type MaxHeap struct {
*heap.Heap
}
// New : returns a new instance of a Heap
func New(input []int) *MaxHeap {
h := &MaxHeap{
&heap.Heap{
Items: input,
},
}
if len(h.Items) > 0 {
h.buildMaxHeap()
}
return h
}
func (h *MaxHeap) buildMaxHeap() {
for i := len(h.Items)/2 - 1; i >= 0; i-- {
h.maxHeapifyDown(i)
}
}
// Insert : adds an element to the heap
func (h *MaxHeap) Insert(item int) *MaxHeap {
h.Items = append(h.Items, item)
lastElementIndex := len(h.Items) - 1
h.maxHeapifyUp(lastElementIndex)
return h
}
// ExtractMax : returns the maximum element and removes it from the Heap
func (h *MaxHeap) ExtractMax() int {
if len(h.Items) == 0 {
log.Fatal("No items in the heap")
}
minItem := h.Items[0]
lastIndex := len(h.Items) - 1
h.Items[0] = h.Items[lastIndex]
// shrinking slice
h.Items = h.Items[:len(h.Items)-1]
h.maxHeapifyDown(0)
return minItem
}
func (h *MaxHeap) maxHeapifyUp(index int) {
for h.HasParent(index) && h.Parent(index) < h.Items[index] {
h.Swap(h.GetParentIndex(index), index)
index = h.GetParentIndex(index)
}
}
func (h *MaxHeap) maxHeapifyDown(index int) {
// iterate until we have a child node smaller than the index value
for (h.HasLeft(index) && h.Items[index] < h.Left(index)) ||
(h.HasRight(index) && h.Items[index] < h.Right(index)) {
// if both children are smaller
if (h.HasLeft(index) && h.Items[index] < h.Left(index)) &&
(h.HasRight(index) && h.Items[index] < h.Right(index)) {
// compare the children and swap with the largest
if h.Left(index) > h.Right(index) {
h.Swap(index, h.GetLeftIndex(index))
index = h.GetLeftIndex(index)
} else {
h.Swap(index, h.GetRightIndex(index))
index = h.GetRightIndex(index)
}
// else if only left child is smaller than swap with it
} else if h.HasLeft(index) && h.Items[index] < h.Left(index) {
h.Swap(index, h.GetLeftIndex(index))
index = h.GetLeftIndex(index)
// else it must be the right child that is smaller, so we swap with it
} else {
h.Swap(index, h.GetRightIndex(index))
index = h.GetRightIndex(index)
}
}
}
Once you got your head around the Max Heap, try to have a look at the Min Heap implementation and see what the differences are. There are very few.
If you think you have a better way of doing any of the parts above, please feel free to make a PR!
Happy data structuring! :)
Video







Top comments (0)