Nesse artigo vou explicar o que eu considero como primeiro passo no mundo do Machine Learning: as Regressões. Mas primeiro vamos entender o conceito de regressão linear.
Em uma visão bem simplista uma regressão é a melhor linha que descreve a relação entre alguns dados.
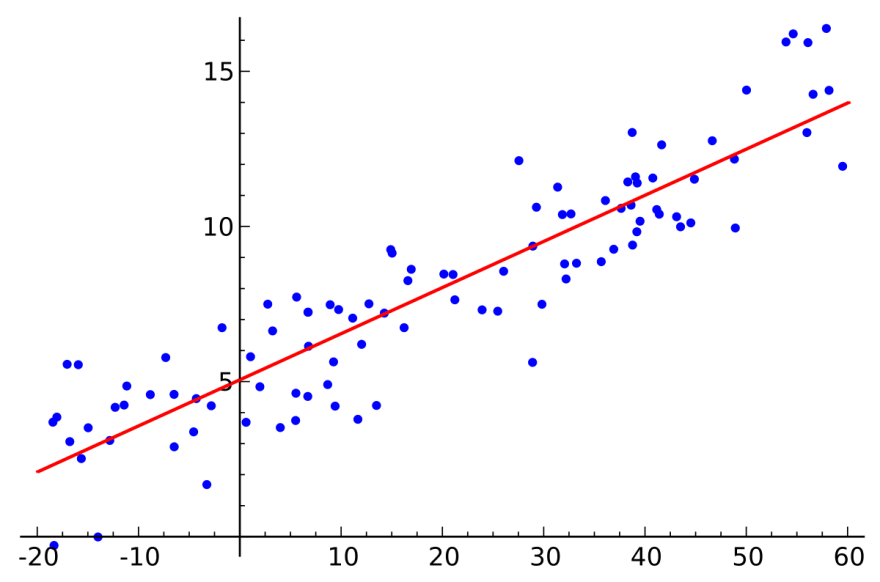 Reta de regressão linear simples
Reta de regressão linear simples
Esses dados se dividem em variável dependente, que é a variável que vamos predizer, é a nossa resposta, e uma ou mais variáveis independentes que são as que vamos utilizar para entender a relação e conseguir os resultados.
Quando ouvimos falar de modelos regressivos, em geral, estamos falando de variáveis dependentes quantitativas. Mas isso não é regra existem regressões para variáveis dependentes qualitativas, como a Regressão Logística.
Apesar de nesse artigo eu descrever apenas regressões lineares (“retas”) existem regressões para descrever relações não-lineares também.
Agora, uma regressão serve apenas predizer valores? Não.
O que uma regressão pode nos dizer?
- Existe relação entre a minha variável dependente (resposta) e a outras variáveis?
- Quão forte é a relação das variáveis com a variável resposta?
- Qual delas contribui mais para variável resposta?
- O quanto cada variável afeta a variável resposta?
- Essa relação é realmente linear?
- Quão acurado conseguimos predizer a variável resposta?
Além disso tudo as regressões são modelos explicáveis, ou seja, não são uma caixa-preta que ninguém entende o porquê daquela resposta e dependendo do assunto essa explicabilidade é mais importante do que uma boa acurácia nas predições.
Regressão Linear Simples
Uma regressão tem a cara dessa equação aqui (uma equação de reta):
Y ≈ α + βX.
Onde Y é a variável dependente, que irá ser predita, X é a minha variável independente, o nosso preditor e α e β são coeficientes/parâmetros que o modelo vai tentar encontrar. Exemplificando: Y podem ser as vendas de uma empresa e X o valor gasto com uma campanha de marketing, assim conseguimos identificar quanto o gasto com marketing pode influenciar nas vendas.
Lembrem que a regressão quer encontrar melhor reta que descreve a relação entre os dados e para isso é preciso entrar os melhores α e β.
Para encontrar os coeficientes, essa equação y = a + bx é feita para cada ponto do dataset gerando vários y, a, b estimados. Como o modelo não é perfeito y estimado vai ser diferente do Y real que temos no dataset e essa diferença é chamada de resíduo. O objetivo de uma regressão é então encontrar uma reta com os menores resíduos possíveis.
Veja que na primeira equação eu escrevi aproximado ≈ e não igual =, porque a equação completa ainda é somada com os erros acarretados das estimativas.
Y = α + βX + Є.
Existem algumas formas diferentes de calcular o erro final do modelo para que ele não fique enviesado e que seja possível medir a qualidade do nosso modelo, entretanto vou explicar uma das mais simples aqui chamada de Média dos Erros ao Quadrado (MSE) que é a soma dos resíduos ao quadrado, ou seja, para cada resíduo de cada ponto iremos colocá-lo ao quadrado e somar todos eles, dividido pelo número de observações. Portanto, esse modelo vai procurar pela reta que possui o menor MSE e declará-la como a que melhor descreve essas relações.
Não foi tão difícil né?
Regressão Linear Múltipla
Agora essa fica bem fácil, pois funciona da mesma forma que a simples só que é usada para mais do que uma variável independente.
Y = α + βX1 + γX2+ Є.
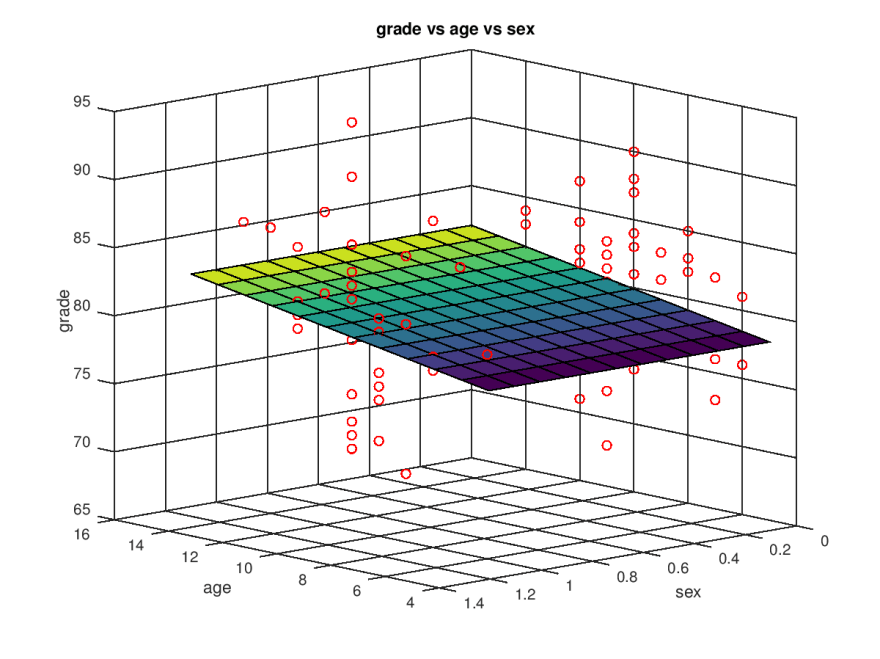
Plano de regressão linear múltipla
fonte: http://marcelojo.org/2017/10/multiple-linear-regression.html
Nesse exemplo a gente conseguiria entender a escolaridade de alguém (grade) usando a idade (age) e o gênero.
Bom, agora a gente já entendeu como funciona uma regressão, mas ainda não sabemos como responder todas aquelas perguntas do começo do artigo. A maioria delas pode ser respondida olhando para os coeficientes e o erro da nossa equação.
O erro é o que a gente perde com o modelo, já que , no geral, as relações não são exatamente lineares. Por exemplo, se estamos predizendo algum preço, em reais, e o erro final ficou no valor de 200, isso significa que o modelo provavelmente vai errar o valor predito em 200 reais em média.
Já os coeficientes conseguem nos explicar justamente o quão forte aquela variável se relaciona com a variável resposta, ou seja, a variável independente que tiver o maior coeficiente será a variável que mais contribui para esse modelo. Além disso, cada coeficiente vai representar o quanto em média a variável resposta vai mudar para cada unidade da sua variável dependente. Por exemplo, se a nossa resposta for a altura, em cm, de uma pessoa nos baseando em variáveis como idade e peso, observando o coeficiente da idade em 20 significa que para cada ano adquirido uma pessoa cresce em média 20 cm (isso com o peso constante).
Referências
Vou deixar um livro que usei para aprender algumas técnicas, não só regressão, e também um canal que eu gosto muito e explica estatística de forma bem didádica (em inglês 🙁)
An Introduction to Statistical Learning — Gareth James et al






Top comments (0)