Searching and Sorting are fundamental bases of programming and all programmers has at some time needed to implement an algorithm that traverses a list or array of information.
There are many ways to do this, and today, we're going to talk about the most powerful search known as Binary Search.
What is a Binary Search?
Is a search algorithm that find the position of multiple elements using some target. Binary search is faster than linear seach and only works in a sorted set of elements.
How it works?
The main idea is to split the array in half and fetch the target element from the first part of the array. If it exists, the other half will be discarded. This makes this approach much faster than any other search model.
Imagine that we have an array of 8 elements as shown in the following image:

We want to check if the number 16 exists in the array and return its position in the array. In this example, we have the element present in position 5.
What binary search does is split the array in two and check if the target is present in the first part of the split:
In this step the algorithm compares the element we are looking for with the middle value of the array. If they are unequal, eliminate half and look for the other half.
Hands On
Let’s put it into practice by creating an example in Java that does exactly what was said above:
public int binarySearch(int[]array, int target, int low, int high) {
int middlePosition = (low + high) / 2;
int currentNumber = array[middlePosition];
if (low > high) {
return -1;
}
if (target == currentNumber) {
return middlePosition;
}
if (target < currentNumber) {
return binarySearch(array, target, low, middlePosition - 1);
} else {
return binarySearch(array, target, middlePosition + 1, high);
}
}
If you notice, we use the recursion technique instead of the conventional while.
Let’s understand what’s next. First we create a method binarySearch that receives an array, the target we are looking for and two arguments low, high.
binarySearch(int[]array, int target, int low, int high) {
}
The param low will be the first index of our array, the first time it will always be 0 and high the array size -1.
Next, we create a middlePosition and currentPosition variable that will store the value of the calculation, which means ( low(0) + high(7)) / 2.
int middlePosition = (low + high) / 2;
int currentNumber = array[middlePosition];
This value will be equivalent to 3, exactly the middle of the array. Note that here, we are talking about the position of the array 3 which is equivalent to the number 8.
In the sequence we have the first validation that means that we haven’t found our target within the array and we will return -1 indicating that it was not found.
if (low > high) {
return -1;
}
Next, we have to verify if the target is exactly the same as the middle position of the array, if so, we found our element and finish our search.
if (target == currentNumber) {
return middlePosition;
}
After these two validations, we will actually start the binary search with recursion.
if (target < currentNumber) {
return binarySearch(array, target, low, middlePosition - 1);
} else {
return binarySearch(array, target, middlePosition + 1, high);
}
Notice that in the first iteration, our target(16) is not less than currentNumber(8) (position 3 of the array), so our code goes to the else calling the function again and setting the low variable with value 4 middlePosition (3) + 1 = 4, causing our search to go to the right side and reach position 4.
Next our code goes to thevalue 16 and thus returning its index.
Now, lets test our function:
@Test
public void should_return_position_5_when_target_is_16() {
int[] array = {3, 5, 7, 8, 13, 16, 17, 20};
int target = 16;
BinarySearch b = new BinarySearch();
int position = b.binarySearch(array, target, 0, array.length - 1);
Assertions.assertEquals(position, 5);
}
@Test
public void should_return_minus1_when_target_is_notFound() {
int[] array = {3, 5, 7, 8, 13, 16, 17, 20};
int target = 33;
BinarySearch b = new BinarySearch();
int position = b.binarySearch(array, target, 0, array.length - 1);
Assertions.assertEquals(position, -1);
}
Notice that we created two tests. First to verify if the target 16 is in our array. And the second test, to validate if we send an element that doesn’t exists on array it’s return -1.
Efficiency: Simple Loop x Binary Search
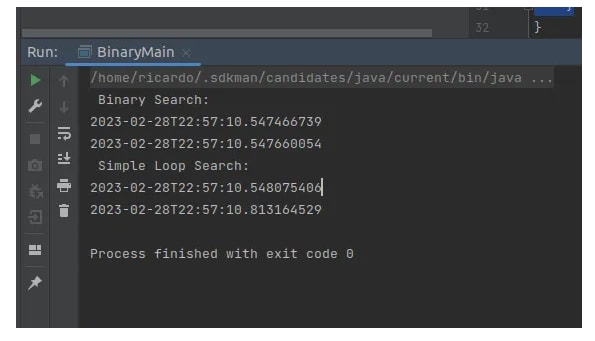
As we mentioned earlier, binary search is much more powerful and efficient than conventional loop searches. Let's take a look at performance by creating an array of size 700000000 and search an element using simple loop and a binary search approaches:
Simple Loop:
public class SimpleLoopSearch {
public int searchNumberPosition(int[] array, int target) {
for (int i = 0; i < array.length; i++) {
if (array[i] == target) {
return i;
}
}
return -1;
}
}
Main
public static void main(String[] args) {
int[] array = new int[700000000];
int target = 680000000;
for (int i=0; i<array.length; i++) {
array[i] = i + 1;
}
BinarySearch b = new BinarySearch();
System.out.println(" Binary Search: ");
System.out.println(LocalDateTime.now());
b.binarySearch(array, target, 0, array.length - 1);
System.out.println(LocalDateTime.now());
System.out.println(" Simple Loop Search: ");
SimpleLoopSearch s = new SimpleLoopSearch();
System.out.println(LocalDateTime.now());
s.searchNumberPosition(array, target);
System.out.println(LocalDateTime.now());
}
After running this code, we will notice that there was a nanosecond difference between the two approaches, where the binary search had no impact on time
Conclusion
Binary search is an important tool for dealing with large amounts of data. It’s an efficient, reliable and indispensable approach in computer science.
Feel free to suggest changes or contribute to the project.
You can find the complete source code for this example on my gitHub. Thanks ❤️







Top comments (0)