Binary Search

• As we saw previously, we looked at the linear search and how it is able to find a target element by iterating over each and every element in the array

• Well, binary search is the second most fundamental search algorithm after linear search.

NB: While in linear search we have to find each element from an array by checking each and every element of this array. This means we have to continue iterating over every element until we find the element we are searching for or until we have reached the dead-end of the array.

Algorithm:

    arr = [2, 4, 6, 9, 11, 12, 14, 20, 36, 48] (Sorted array)
    target = 36
1. Find the middle element
2. Check:
    If target > middle => search in right else => search in left
3. if target == middle => we found element

Example:

Here, the space in which we are searching is getting divided into spaces.

Time complexity:

Best case: O(1)
Worst case: O(logn)

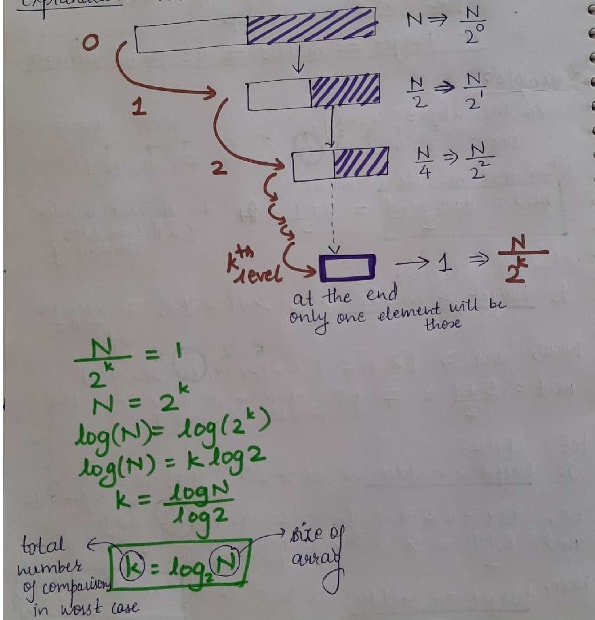
Explanation: find the maximum number of comparisons

=> Order agnostic Binary search

• Let's say if we don't know that the array is sorted in ascending or descending order.

  arr = [90, 75, 18, 12, 6, 4, 3, 1]
  target = 75

Here, target > middle => search in left

Here, start > end -> Descending order
90 > 1
when start < end -> Ascending order

For further explanation about Binary search algorithm, kindly check out this wonderful toturial.
Binary Search in Java by Kunal Kushwaha

Feel free to connect with me on github and Linkedin, thank you.