Advent of Code 2021 Day 23
Solve for X where X equals...
- An integer that is greater than and as close as possible to the minimum unobstructed score after solving the puzzle
That's our output. What's our input?
- A multi-line string
- Consisting of 6 possible characters
#.ABCD
What does our input represent?
- A hallway and four rooms
- The stage for playing a game akin to Towers of Hanoi
How do we win this game?
- Move the letters
A,B,C,Dsuch that each of the four rooms - from left to right - contains only one type of letter organized alphabetically - Achieve the smallest possible score (see scoring in the next section). Strategically speaking: move D's as few times as possible, and move A's more often than any other character.
How do we play this game?
- Abide by all three movement constraints: 1) Any letter can move at most twice - either directly from its starting location into its destination room, or with a stop in the hallway in between; 2) Letters cannot stop on spaces directly north of each room; 3) Letters cannot enter any room other than their destination room, and can only enter that room when empty or when the other letters in that room are each of the correct type
- Keep track of a running score that accounts for each letter type's move cost:
A costs 1 to move,B costs 10 to move,C costs 100 to move,D costs1000 to move`
Why there are no algorithms in this article
- It took me several hours in a day just to solve Part 1 with pen and paper
- It took me even more hours in a day to solve Part 2 using a Design tool on my computer where I re-created the game board and moved text layers around to simulate playing
- When scouring GitHub and Reddit for coded solutions, they were each far too complex for me to understand, let alone attempt to re-create
- Given how difficult it was to solve these puzzles by hand, I recognize how unprepared I am to attempt to codify even an inefficient, brute-force algorithm that discovers the same minimum solution
Part 1
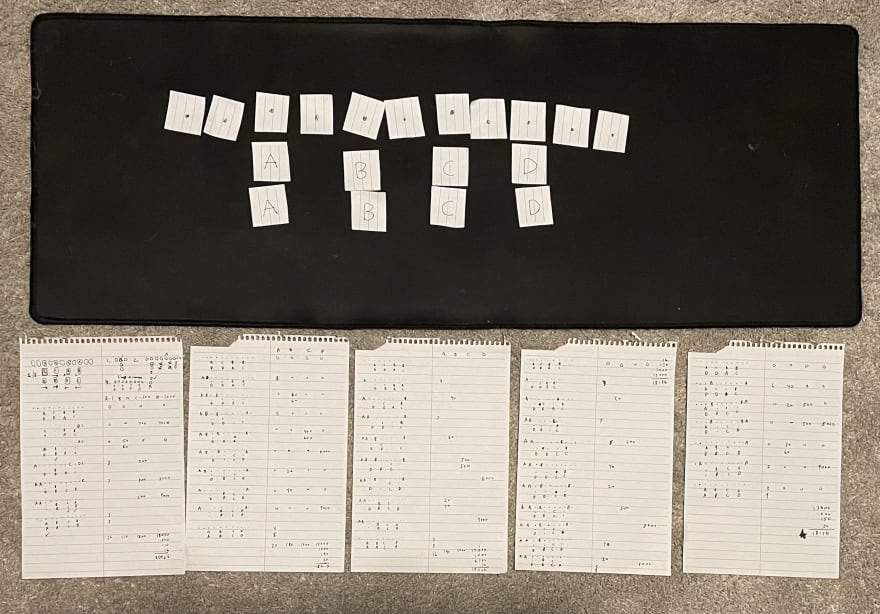
- What follows are my hand-drawn notes from solving Part 1 with the input generated for me
Visualization created using Amphipod.net

My process: hand-drawn
First successful attempt: 20926 energy, too high

Second successful attempt: 18210 energy, too high

At this point, I needed to move pieces around for real

Third successful attempt: 18206 energy, too high

Fourth successful attempt: 18186 energy, too high

Fifth successful attempt: 18170 energy, correct!

The full collection of artifacts that led to my discovery of the correct answer
Part 2
- I must have tried hundreds of times
- I kept trying to solve it by starting with the two C's in the second room
- It wasn't until late in the day that I started by emptying the 2 B's and 2 A's in room three
- To all fellow beginner puzzlers, know that what you don't see below are all the Quicktime recordings (and the thousands of Undo commands) representing my failed attempts to solve Part 2
Visualization created using Amphipod.net

My process: Moving text layers in Sketch
- It was going to be too much work to move pieces of paper around
- Instead, I recreated the game board using a design tool called Sketch
- This way, I could freely attempt to play the game, and press 'Undo' as many times as needed to 'reset' the game board
- Also, I could record my attempts at any time using Quicktime. If it didn't teach me anything, I could just throw the video away and reset the game board in seconds, not minutes.
Save for later
- Study Dijkstra's algorithm, as that was the 'shortest path' algorithm most-often referenced by other solvers




Top comments (0)