Advent of Code 2017 Day 14
Try the simulator with your puzzle input!
Part 1
- It makes sense now!
- Using my knot hasher to solve
Day 10 Part 3
It makes sense now!
- I wondered if I needed to complete Day 10's puzzle before attempting today's puzzle
- I knew I needed to turn some string of characters into a 128-bit binary number
- I knew hexadecimal numbers were involved
- I was confused how to get from a string comprised of letters other than
a-fto something based on hexadecimals - That's where I hopped over to Day 10
Thankfully, I solved both parts of Day 10!
And I return to Day 14 with a working knot hash maker!
I think I'm ready to use it to generate the 128-bit numbers required for this puzzle.
Using my knot hasher to solve Day 10 Part 3
- My algorithm from Day 10 Part 2 takes any string of text as input and generates a 32-character string containing only
0-9,a-fas characters
In Part 1, I must use it like this:
Create an array with 128 elements
Where each element eventually becomes a string of 0s and 1s
As a result of the following operations:
1. Build a string using the pattern: input dash index
2. Pass it as input to my knot hashing algorithm
3. Split the resulting string into an array of single characters
4. Update each character to the result of converting that character to its hexadecimal value, then to its binary value, then prefixing it with as many 0s necessary to make it 4 characters long
5. Concatenate each resulting character together into a string of 0s and 1s
Accumulate a sum, starting at 0, of the amount of 1s in each string by adding all the number-coerced values together
It's one long chain of string and array methods including map(), split(), join(), reduce(), toString() and padStart().
Operation #4 above required me to search for:
[programming language] convert hex to binary
Which guided me toward the same Stack Overflow answer I found during Day 10:
parseInt(hex,16).toString(2).padStart(4,0)
The padStart() ensures the binary number is four characters long - adding 0s where appropriate.
Testing my algorithm:
- It works on the example string!
- It works on my puzzle input!
Part 2
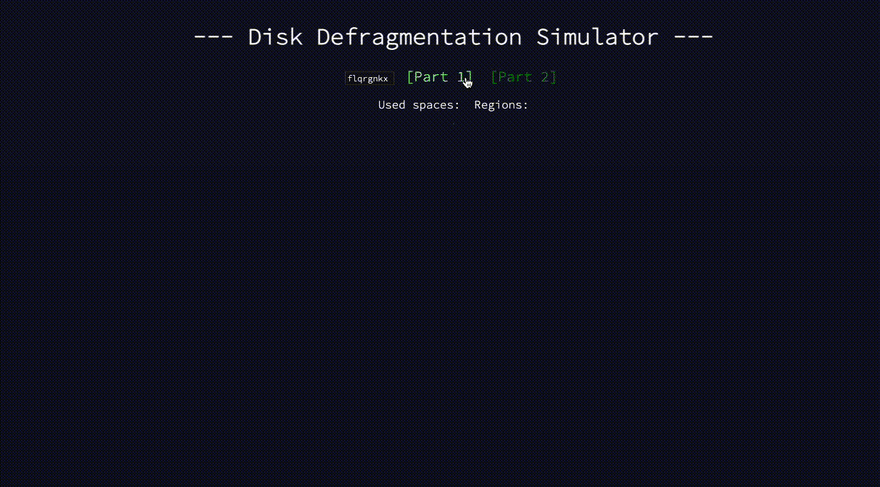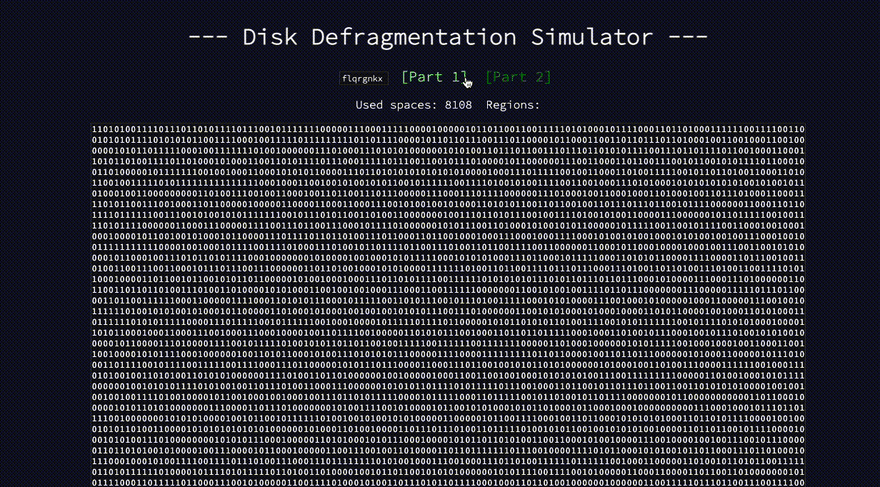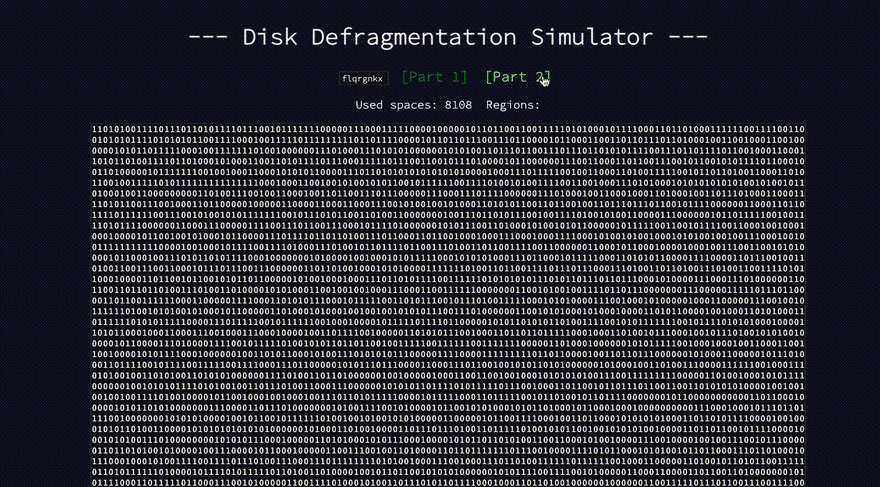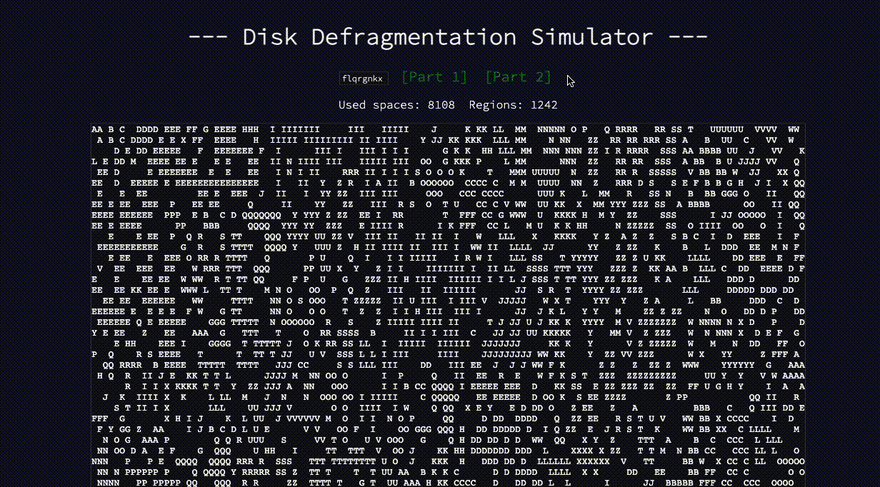
- Recursive adjacent cells algorithm, here I come!
- But first, a simulator!
- Cheating...except not really
- Updating the simulator
Recursive adjacent cells algorithm, here I come!
- I'm reminded of 2021 Day 9's Part 2 puzzle
- It required the identification and sizing of smoke basins within a large grid
- Except, there the borders were marked by
9 - Whereas, here the borders are marked by
. - I'm really hopeful that I can re-use my working algorithm from that part, update a few conditions, and generate the correct answer for this puzzle
But first, a simulator!
- Mostly because I want to see the 128x128 grid
- And because I anticipate building a simulator for both parts, since they are highly visual
Time to build one that shows the grid!
...
Wow, that was the quickest one I've built yet!
Mainly because I just copied and tweaked the one I made for Smoke Basin.
After implementing Part 1, I saw this for the example input:

Cheating...except not really
- As mentioned above, I wrote a working recursive-adjacent-cell-tracking algorithm as part of 2021 Day 9 Part 2's puzzle
- It was now time to test it's reusability under slightly different rules
- I changed conditions where I checked for
9to check for0 - I updated a few variable names
- And I returned the length of the list containing the sizes of each region
Much to my delight:
- It worked on the example input!
- It worked on my puzzle input!
Horray for working on these puzzles in reverse-chronological order!
Updating the simulator
- Just like the algorithm, my simulator for 2021 Day 9's puzzle does exactly what I need it to do
- So, I just had to change a few variable names again
I did it!!
- I solved both parts!
- I re-used algorithms and simulators I wrote and built for another puzzle to make Part 2 seem like cheating!
- It feels like I solved Parts 3 and 4 of one long-winded string conversion puzzle!
- I got a ton of practice converting numbers, creating arrays, leveraging indices and the modulo operator, and using higher-order methods as usual




Top comments (0)