The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return the number of distinct solutions to the n-queens puzzle.
Example 1:
Input: n = 4
Output: 2
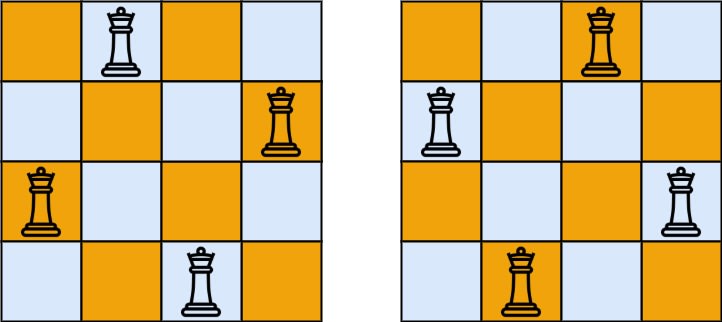
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.
Example 2:
Input: n = 1
Output: 1
Constraints:
-
1 <= n <= 9
SOLUTION:
class Solution:
def getAllPos(self, usedCols, usedPosDiag, usedNegDiag, i, n):
if i >= n:
return [[]]
op = []
for j in range(n):
if j not in usedCols and (i + j) not in usedPosDiag and (i - j) not in usedNegDiag:
val = self.getAllPos(usedCols.union({j}), usedPosDiag.union({i + j}), usedNegDiag.union({i - j}), i + 1, n)
op += [[j] + v for v in val]
return op
def getRow(self, i, n):
val = ["."] * n
val[i] = "Q"
return "".join(val)
def totalNQueens(self, n: int) -> int:
queens = self.getAllPos(set(), set(), set(), 0, n)
return len(queens)


Top comments (0)