On an 8x8 chessboard, there can be multiple Black Queens and one White King.
Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.
Example 1:
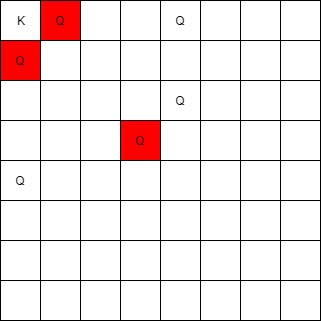
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:
The queen at [0,1] can attack the king cause they're in the same row.
The queen at [1,0] can attack the king cause they're in the same column.
The queen at [3,3] can attack the king cause they're in the same diagnal.
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1].
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0].
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.
Example 2:
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]
Example 3:
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]
Constraints:
-
1 <= queens.length <= 63 -
queens[i].length == 2 -
0 <= queens[i][j] < 8 -
king.length == 2 -
0 <= king[0], king[1] < 8 - At most one piece is allowed in a cell.
SOLUTION:
class Solution:
def isValid(self, x, y):
if x < 0 or y < 0 or x >= 8 or y >= 8:
return False
return True
def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:
x, y = king
queens = set([tuple(q) for q in queens])
op = []
for dx, dy in [(1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1), (1, -1)]:
n = 1
while self.isValid(x + n * dx, y + n * dy):
if (x + n * dx, y + n * dy) in queens:
op.append([x + n * dx, y + n * dy])
break
n += 1
return op




Top comments (0)